Chapter 1. Vectors

“Roger, Roger. What’s our vector, Victor?”

— Captain Oveur (Airplane)

This book is all about looking at the world around us and coming up with clever ways to simulate that world with code. Divided into three parts, the book will start by looking at basic physics—how an apple falls from a tree, a pendulum swings in the air, the earth revolves around the sun, etc. Absolutely everything contained within the first five chapters of this book requires the use of the most basic building block for programming motion—the vector. And so this is where we begin our story.

Now, the word vector can mean a lot of different things. Vector is the name of a New Wave rock band formed in Sacramento, CA in the early 1980s. It’s the name of a breakfast cereal manufactured by Kellogg’s Canada. In the field of epidemiology, a vector is used to describe an organism that transmits infection from one host to another. In the C# programming language, a vector is an implementation of a dynamically resizable array data structure. While all these definitions are interesting, they’re not what we’re looking for. What we want is called a Euclidean vector (named for the Greek mathematician Euclid and also known as a geometric vector). When you see the term “vector” in this book, you can assume it refers to a Euclidean vector, defined as an entity that has both magnitude and direction.

A vector is typically drawn as a arrow; the direction is indicated by where the arrow is pointing, and the magnitude by the length of the arrow itself.

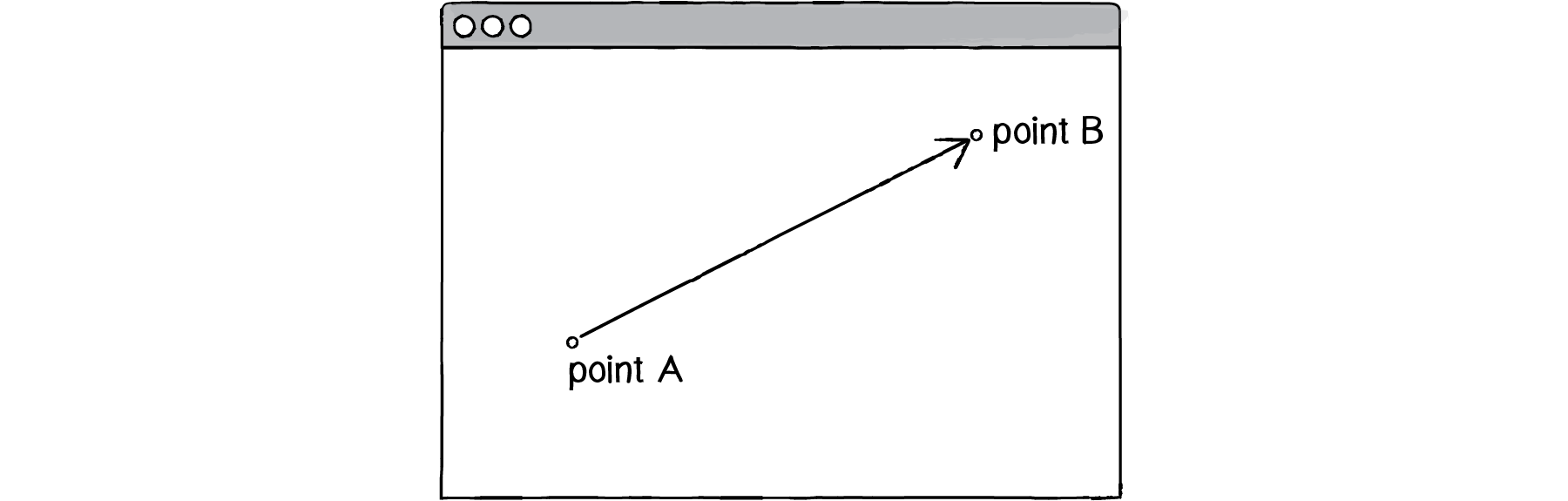
Figure 1.1: A vector (drawn as an arrow) has magnitude (length of arrow) and direction (which way it is pointing).

In the above illustration, the vector is drawn as an arrow from point A to point B and serves as an instruction for how to travel from A to B.

1.1 Vectors, You Complete Me

Before we dive into more of the details about vectors, let’s look at a basic Unity example that demonstrates why we should care about vectors in the first place. If you’ve read any introductory C# textbooks or taken a class on programming with Unity (and hopefully you’ve done one of these things to help prepare you for this book), you probably, at one point or another, learned how to write a simple bouncing mover scene.

Example 1.1: Bouncing mover with no vectors

• Code
• Demo

In the above example, we have a very simple world—a blank canvas with a circular shape (a “mover”) traveling around. This mover has some properties, which are represented in the code as variables.

In a more advanced scene, we could imagine having many more variables:

It’s becoming clearer that for every concept in this world (wind, location, acceleration, etc.), we’ll need two variables. And this is only a two-dimensional world. In a 3D world, we’ll need x, y, z, xSpeed, ySpeed, zSpeed, and so on. Wouldn’t it be nice if we could simplify our code and use fewer variables? Instead of:

    private float x;
    private float y;

    private float xSpeed = .03f;
    private float ySpeed = .03f;
    

We could simply have…

    Vector2 location;
    Vector2 speed;
    

Taking this first step in using vectors won’t allow us to do anything new. Just adding vectors won’t magically make your Unity experiences simulate physics. However, they will simplify your code and provide a set of functions for common mathematical operations that happen over and over and over again while programming motion.

1.2 Vectors for Unity Programmers

One way to think of a vector is the difference between two points. Consider how you might go about providing instructions to walk from one point to another.

Here are some vectors and possible translations:

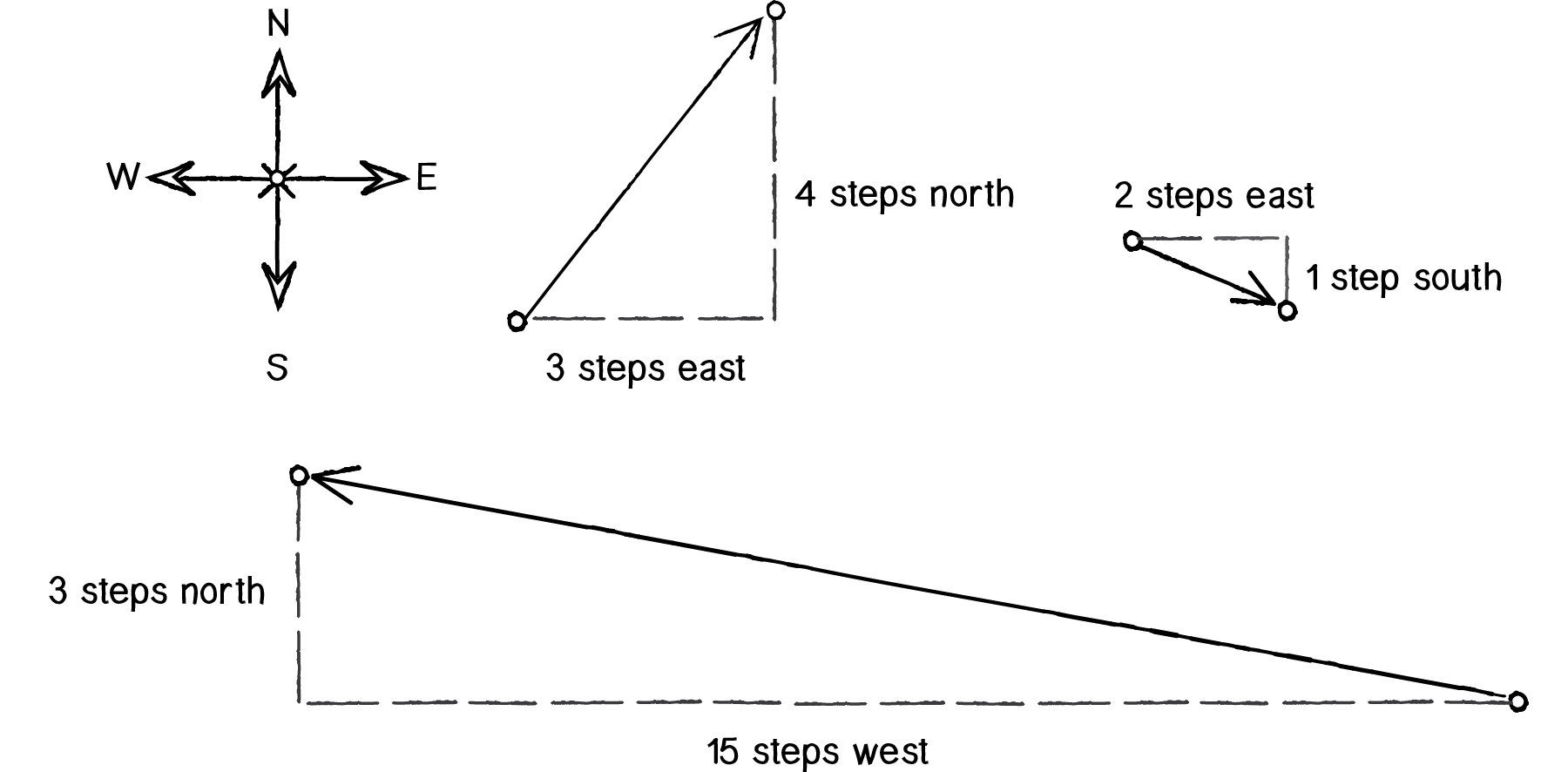
• (-15, 3) - Walk fifteen steps west; turn and walk three steps north.
• (3, 4) - Walk three steps east; turn and walk five steps north.
• (2, -1) - Walk two steps east; turn and walk one step south.

You’ve probably done this before when programming motion. For every frame of animation (i.e. a single cycle through Unity’s Update() loop), you instruct each object on the screen to move a certain number of units horizontally and a certain number of units vertically.

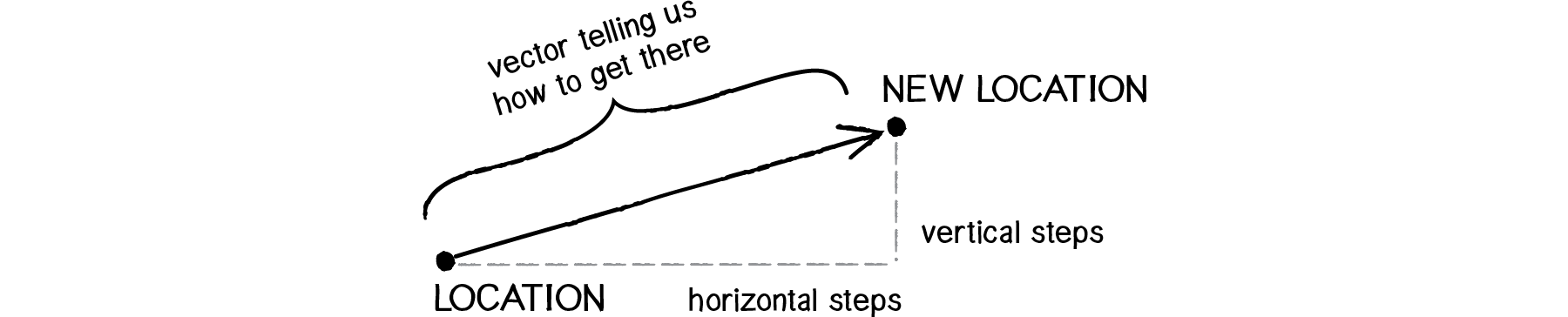
For every frame:

new location + velocity applied to current location

If velocity is a vector (the difference between two points), what is location? Is it a vector too? Technically, one might argue that location is not a vector, since it’s not describing how to move from one point to another—it’s simply describing a singular point in space.

Nevertheless, another way to describe a location is the path taken from the origin to reach that location. Hence, a location can be the vector representing the difference between location and origin.

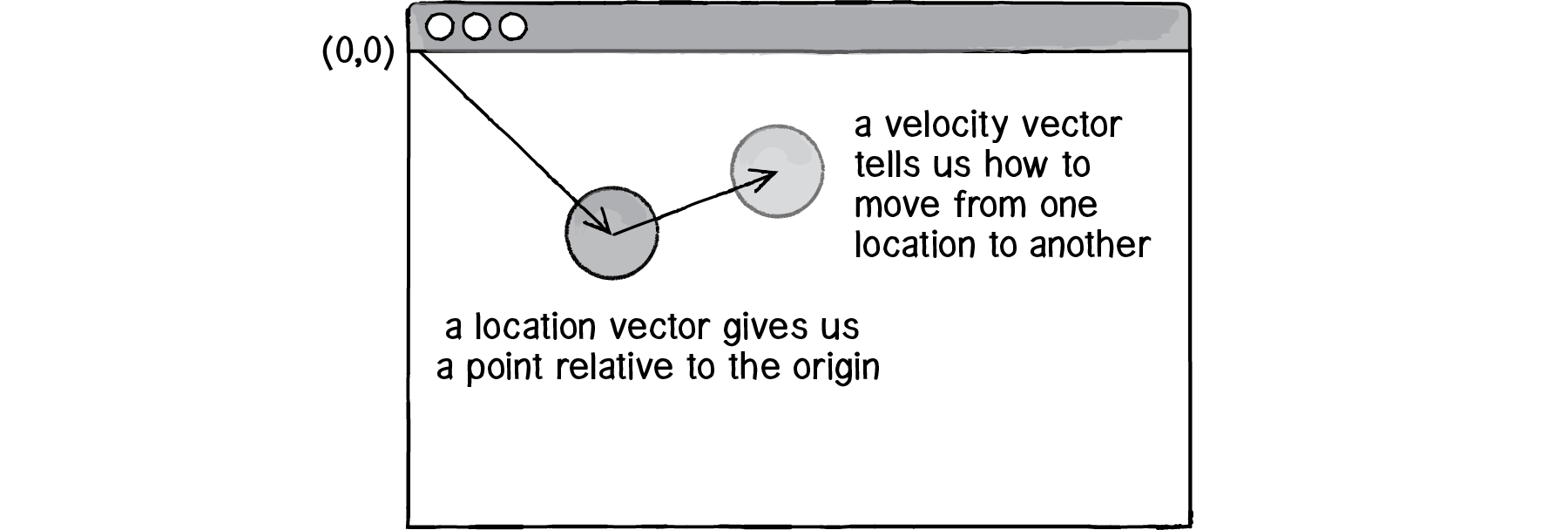
Let’s examine the underlying data for both location and velocity. In the bouncing mover example, we had the following:

Notice how we are storing the same data for two floating point numbers, an x and y. If we were to write a vector class ourselves, we’d start with something rather basic:

    public class Vector2
    {
        public float x;
        public float y;

        public Vector2(float x_, float y_)
        {
            x = x_;
            y = y_;
        }
    }
    

At its core, a Vector2 is just a convenient way to store two values.

And so this …

    private float x;
    private float y;

    private float xSpeed = .03f;
    private float ySpeed = .03f;
    

becomes …

    private Vector2 location = new Vector2(0f, 0f);
    private Vector2 velocity = new Vector2(0.3f, 0.3f);
    

Now that we have two vector objects (location and velocity), we’re ready to implement the algorithm for motion—location += velocity. In Example 1.1, without vectors, we had:

    x += xSpeed;
    y += ySpeed;
    

In Unity, we could rewrite the above as:

    location += velocity;
    

However, let's look deeper at the math of how we add two different Vector objects.

1.3 Vector Addition

Before we continue looking at the Vector2 class and its addVectors() method (purely for the sake of learning since it’s already implemented for us in Unity itself as an operator of Vector2), let’s examine vector addition using the notation found in math and physics textbooks.

Vectors are typically written either in boldface type or with an arrow on top. For the purposes of this book, to distinguish a vector from a scalar (scalar refers to a single value, such as an integer or a floating point number), we’ll use an arrow on the right or on top for notation:

• Vector: u→
• Scalar: x

Let’s say I have the following two vectors:

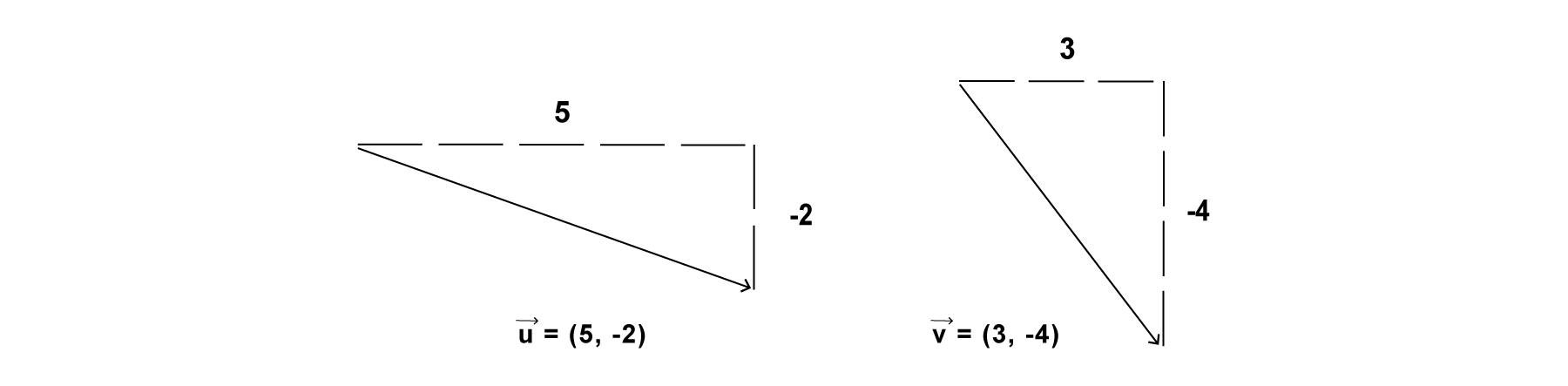
Each vector has two components, an x and a y. To add two vectors together, we simply add both x’s and both y’s.

In other words:

w→=u→+v→

can be written as:

w.x=u.x+v.x

Then, replacing u and v with their values from Figure 1.6, we get:

w.x=5+3

w.y=-2+-4

which means that:

w.x=8 w.y=-6

Finally, we write that as a vector:

w→=(8,-6)

Now that we understand how to add two vectors together, we can look at how addition is implemented in the Vector2 class itself. Let’s write a function called AddVectors() that takes another Vector2 object as its argument.

    Vector2 AddVectors(Vector2 vectorA, Vector2 vectorB)
    {
        float newX = vectorA.x + vectorB.x;
        float newY = vectorA.y + vectorB.y;
        return new Vector2(newX, newY);
    }
    

Now that we see how AddVectors() is written inside of Vector2, we can return to our bouncing mover example with its location + velocity algorithm and implement vector addition

    location = AddVectors(location, velocity);

    //While this is perfectly acceptable, in Unity,
    //we will write this with built in vector arithmetic so everything plays nice.

    location += velocity;
    

And here we are, ready to rewrite the bouncing mover example using Vector2.

Example 1.2: Bouncing mover with Vector2s!

• Code
• Demo

Now, you might feel somewhat disappointed. After all, this may initially appear to have made the code more complicated than the original version. While this is a perfectly reasonable and valid critique, it’s important to understand that we haven’t fully realized the power of programming with vectors just yet. Looking at a simple bouncing mover and only implementing vector addition is just the first step. As we move forward into a more complex world of multiple objects and multiple forces (which we will introduce in Chapter 2), the benefits of Vector2 will become more apparent.

We should, however, note an important aspect of the above transition to programming with vectors. Even though we are using Vector2 objects to describe two values—the x and y of location and the x and y of velocity—we still often need to refer to the x, y (and z for Vector 3) components of each Vector2 individually. This is done through standard OOP dot notation, ie location.x or velocity.y.

1.4 More Vector Math

Addition was really just the first step. There are many mathematical operations that are commonly used with vectors. Below is a comprehensive list of the operations available as functions in the Vector2 class. We’ll go through a few of the key ones now. As our examples get more sophisticated in later chapters, we’ll continue to reveal the details of more functions.

• Subtraction: -
• Addition: +
• Multiplication: *
• Division: /
• Returns true if vectors are different: !=
• Returns true if values are approximately equal: ==
• Returns the length of this vector: Vector2.magnitude
• Returns this vector with a magnitude of 1: Vector2.normalized
• Returns the angle in degrees between from and to: Angle(Vector2 from, Vector2 to);
• For more visit the Vector2 Documentation for Unity

Having already covered addition, let’s start with subtraction. This one’s not so bad; just take the plus sign and replace it with a minus!

Vector subtraction

w→=u→−v→

can be written as:

w.x=u.x−v.x

w.y=u.y−v.y

Figure 1.7: Vector Subtraction

and so the function inside Vector2 looks like:

    Vector2 SubtractVectors(Vector2 vectorA, Vector2 vectorB)
    {
        float newX = vectorA.x - vectorB.x;
        float newY = vectorA.y - vectorB.y;
        return new Vector2(newX, newY);
    }
    

The following example demonstrates vector subtraction by taking the difference between two points—the mouse location and the center of the window.

Example 1.3: Vector Subtraction

• Code
• Demo

Vector multiplication

Moving on to multiplication, we have to think a little bit differently. When we talk about multiplying a vector, what we typically mean is scaling a vector. If we wanted to scale a vector to twice its size or one-third of its size (leaving its direction the same), we would say: “Multiply the vector by 2” or “Multiply the vector by 1/3.” Note that we are multiplying a vector by a scalar, a single number, not another vector.

To scale a vector, we multiply each component (x and y) by a scalar.

w→=u→*n

can be written as:

w.x=u.x*n

w.y=u.y*n

Let’s look at an example with vector notation.

u→=(−3,-7)

n=3

w→=u→*n

w.x=−3*3

w.y=-7*3

w→=(−9,-21)

Figure 1.8: Scaling a vector

Therefore, the function inside the Vector2 class is written as:

    Vector2 ScaleVector(Vector2 toMultiply, float scaleFactor)
    {
        float x = toMultiply.x * scaleFactor;
        float y = toMultiply.y * scaleFactor;
        return new Vector2(x, y);
    }

    // or

    void Start()
    {
        // make the vector two times longer: prints (2.0, 4.0)
        print(new Vector2(1.0f, 2.0f) * 2.0f);
    }
    

Implementing multiplication in code is as simple as:

    
    location = new Vector2(1.0f, 2.0f);
    ScaleVector(location, 2.0f);

    // or

    new Vector2(1.0f, 2.0f) * 2.0f;
    

Example 1.4: Multiplying a vector

• Code
• Demo

Division works just like multiplication—we simply replace the multiplication sign (asterisk) with the division sign (forward slash).

Figure 1.9:

1.5 Vector Magnitude

Multiplication and division, as we just saw, are means by which the length of the vector can be changed without affecting direction. Perhaps you’re wondering: “OK, so how do I know what the length of a vector is? I know the components (x and y), but how long (in units) is the actual arrow?” Understanding how to calculate the length (also known as magnitude) of a vector is incredibly useful and important.

Figure 1.10: The length or “magnitude” of a vector v→ is often written as: ∥v→∥

Notice in the above diagram how the vector, drawn as an arrow and two components (x and y), creates a right triangle. The sides are the components and the hypotenuse is the arrow itself. We’re very lucky to have this right triangle, because once upon a time, a Greek mathematician named Pythagoras developed a lovely formula to describe the relationship between the sides and hypotenuse of a right triangle.

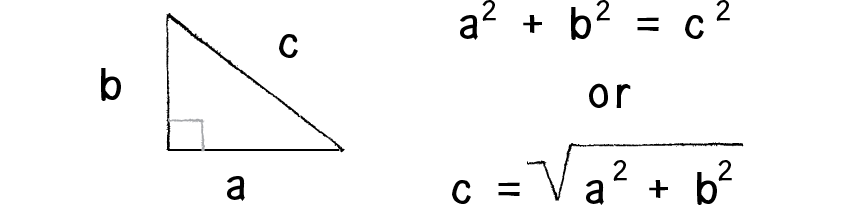
Figure 1.11: The Pythagorean Theorem

The Pythagorean theorem is: a squared plus b squared equals c squared.

Armed with this formula, we can now compute the magnitude of v→ as follows:

    float MagnitudeOf(Vector2 vector)
    {
        float aSquared = vector.x * vector.x;
        float bSquared = vector.y * vector.y;

        float magnitude = Mathf.Sqrt(aSquared + bSquared);

        return magnitude;
    }

    or

    //Returns the length of this vector (Read Only).
    //The length of the vector is square root of (x*x+y*y).
    vectorMagnitude = Vector2.Magnitude(subtractedVector);
    

Example 1.5: Vector Magnitude

• Code
• Demo

1.6 Normalizing Vectors

Calculating the magnitude of a vector is only the beginning. The magnitude function opens the door to many possibilities, the first of which is normalization. Normalizing refers to the process of making something “standard” or, well, “normal.” In the case of vectors, let’s assume for the moment that a standard vector has a length of 1. To normalize a vector, therefore, is to take a vector of any length and, keeping it pointing in the same direction, change its length to 1, turning it into what is called a unit vector.

Since it describes a vector’s direction without regard to its length, it’s useful to have the unit vector readily accessible. We’ll see this come in handy once we start to work with forces in Chapter 2.

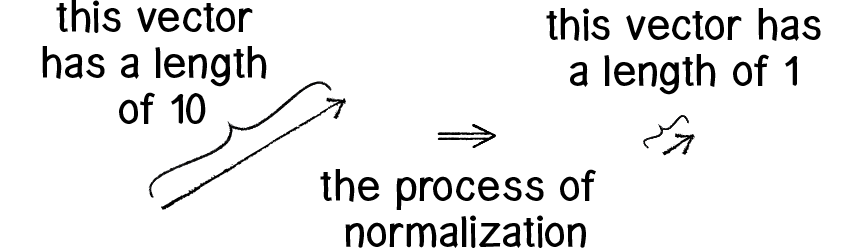
Figure 1.12:

In other words, to normalize a vector, simply divide each component by its magnitude. This is pretty intuitive. Say a vector is of length 5. Well, 5 divided by 5 is 1. So, looking at our right triangle, we then need to scale the hypotenuse down by dividing by 5. In that process the sides shrink, divided by 5 as well.

Example 1.6: Normalizing a vector

• Code
• Demo

1.7 Vector Motion: Velocity

All this vector math stuff sounds like something we should know about, but why? How will it actually help us write code? The truth of the matter is that we need to have some patience. It will take some time before the benefits of using the Vector2 class fully come to light. This is actually a common occurrence when first learning a new data structure. For example, when you first learn about an array, it might seem like much more work to use an array than to just have several variables stand for multiple things. But that plan quickly breaks down when you need a hundred, or a thousand, or ten thousand things. The same can be true for Vector2. What might seem like more work now will pay off later, and pay off quite nicely. And you don’t have to wait too long, your reward will come in the next chapter.

For now, however, we want to focus on simplicity. What does it mean to program motion using vectors? We’ve seen the beginning of this in Example 1.2: the bouncing mover. An object on screen has a location (where it is at any given moment) as well as a velocity (instructions for how it should move from one moment to the next). Velocity is added to location:

    location += velocity * Time.deltaTime;
    

Wait, do you notice that new bit of code? Time.deltaTime?

Time.deltaTime allows us to get the completion time in seconds since the last frame. Using this property allows us to move a GameObject in a direction at a certain number of units per second.

And then we draw the object at that location:

    mover.transform.position = new Vector2(location.x, location.y);
    

This is Motion 101.

• Add velocity to location
• Send object to location

In the bouncing mover example, all of this code happened in a single script. What we want to do now is move towards encapsulating all of the logic for motion inside of a class. This way, we can create a foundation for programming moving objects in Unity. In section I.2 of the introduction, “The Random Walker Class,” we briefly reviewed the basics of object-oriented-programming (“OOP”). Beyond that short introduction, this book assumes experience with objects and classes in Unity.

In this case, we’re going to create a generic Mover class that will describe a thing moving around the screen. And so we must consider the following two questions:

• What data does a mover have?
• What functionality does a mover have?

Our Motion 101 algorithm tells us the answers to these questions. A Mover object has two pieces of data: location and velocity, which are both Vector2 objects.

    public class Mover
    {
        // The basic properties of a mover class
        private Vector2 location, velocity;

        // Gives the class a GameObject to draw on the screen
        private GameObject mover = GameObject.CreatePrimitive(PrimitiveType.Sphere);
    }
    

Its functionality is just about as simple. The Mover needs to move and it needs to be seen. We’ll implement these needs as functions named Step(). We’ll put all of our motion logic code in Step().

    public void Step()
    {
        // Moves the mover // Time.deltaTime is the time passed since the last frame.
        location += velocity * Time.deltaTime;
        

        // Updates the GameObject of this movement
        mover.transform.position = new Vector2(location.x, location.y);
    }
    

We’ve forgotten one crucial item, however: the object’s constructor. The constructor is a special function inside of a class that creates the instance of the object itself. It is where you give instructions on how to set up the object. It always has the same name as the class and is called by invoking the new operator:

    public Mover()
    {
        // Our method for setting the window bounds found below
        FindWindowLimits();

        location = new Vector2(Random.Range(-maximumPos.x, maximumPos.x), Random.Range(-maximumPos.y, maximumPos.y));
        velocity = new Vector2(Random.Range(-2f, 2f), Random.Range(-2f, 2f));

        // We need to create a new material for WebGL
        Renderer r = mover.GetComponent<Renderer>();
        r.material = new Material(Shader.Find("Diffuse"));
    }
    

In our case, let’s arbitrarily decide to initialize our Mover object by giving it a random location and a random velocity.

    location = new Vector2(Random.Range(-maximumPos.x, maximumPos.x), Random.Range(-maximumPos.y, maximumPos.y));

    velocity = new Vector2(Random.Range(-2f, 2f), Random.Range(-2f, 2f));
    

If object-oriented programming is at all new to you, one aspect here may seem a bit confusing. After all, we spent the beginning of this chapter discussing the Vector2 class. The Vector2 class is the template for making the location object and the velocity object. So what are they doing inside of yet another object, the Mover object? In fact, this is just about the most normal thing ever. An object is simply something that holds data (and functionality). That data can be numbers (integers, floats, etc.) or other objects! We’ll see this over and over again in this book. For example, in Chapter 4 we’ll use a class to describe a system of particles. That ParticleSystem object will have as its data a list of Particle objects…and each Particle object will have as its data several Vector2 objects!

Let’s finish off the Little Mover class by incorporating a function to determine what the object should do when it reaches the edge of the window. For now let’s do something simple, and just have it wrap around the edges.

    public void CheckEdges()
    {
        if (location.x > maximumPos.x)
        {
            location.x = -maximumPos.x;
        }
        else if (location.x < -maximumPos.x)
        {
            location.x = maximumPos.x;
        }
        if (location.y > maximumPos.y)
        {
            location.y = -maximumPos.y;
        }
        else if (location.y < -maximumPos.y)
        {
            location.y = maximumPos.y;
        }
    }

    private void FindWindowLimits()
    {
        // We want to start by setting the camera's projection to Orthographic mode
        Camera.main.orthographic = true;

        // For FindWindowLimits() to function correctly, the camera must be set to coordinates 0, 0 for x and y. We will use -10 for z in this example
        Camera.main.transform.position = new Vector3(0, 0, -10);

        // Next we grab the maximum position for the screen
        maximumPos = Camera.main.ScreenToWorldPoint(new Vector2(Screen.width, Screen.height));
    }
    

Here is the entire example for reference:

Example 1.7: Motion 101 (velocity)

• Code
• Demo

1.8 Vector Motion: Acceleration

OK. At this point, we should feel comfortable with two things: (1) what a Vector2 is and (2) how we use Vector2s inside of an object to keep track of its location and movement. This is an excellent first step and deserves a mild round of applause. Before standing ovations and screaming fans, however, we need to make one more, somewhat bigger step forward. After all, watching the Motion 101 example is fairly boring—the circle never speeds up, never slows down, and never turns. For more interesting motion, for motion that appears in the real world around us, we need to add one more Vector2 to our class—acceleration.

The strict definition of acceleration we’re using here is: the rate of change of velocity. Let’s think about that definition for a moment. Is this a new concept? Not really. Velocity is defined as the rate of change of location. In essence, we are developing a “trickle-down” effect. Acceleration affects velocity, which in turn affects location (for some brief foreshadowing, this point will become even more crucial in the next chapter, when we see how forces affect acceleration, which affects velocity, which affects location). In code, this reads:

    public void Update()
    {
        // Speeds up the mover
        velocity += acceleration * Time.deltaTime;

        // Moves the mover
        location += velocity * Time.deltaTime;

        // Updates the GameObject of this movement
        mover.transform.position = new Vector2(location.x, location.y);
    }
    

As an exercise, from this point forward, let’s make a rule for ourselves. Let’s write every example in the rest of this book without ever touching the value of velocity and location (except to initialize them). In other words, our goal now for programming motion is: Come up with an algorithm for how we calculate acceleration and let the trickle-down effect work its magic. (In truth, you’ll find reasons to break this rule, but it’s important to illustrate the principles behind our motion algorithm.) And so we need to come up with some ways to calculate acceleration:

Acceleration Algorithms!

• A constant acceleration
• A totally random acceleration
• Acceleration towards the mouse

Algorithm #1, a constant acceleration, is not particularly interesting, but it is the simplest and will help us begin incorporating acceleration into our code. The first thing we need to do is add another Vector2 to the Mover class and implement a top speed:

    public class Mover
    {
        // The basic properties of a mover class
        private Vector2 location, velocity, acceleration;
        private float topSpeed;
    }
    

Next, incorporate acceleration into the Step() function:

    public void Step()
    {
        // Speeds up the mover
        velocity += acceleration * Time.deltaTime;
    }
    

We’re almost done. The only missing piece is initialization in the constructor.

    public Mover()
    {
        // Vector2.zero is a (0, 0) vector
        location = Vector2.zero; 
        velocity = Vector2.zero;
        acceleration = new Vector2(-0.1f, -1f);
    }
    

Let’s start the Mover object in the middle of the window…

    // Vector2.zero is a (0, 0) vector
    location = Vector2.zero; 
    

…with an initial velocity of zero.

    velocity = Vector2.zero;
    

This means that when the scene starts, the object is at rest. We don’t have to worry about velocity anymore, as we are controlling the object’s motion entirely with acceleration. Speaking of which, according to Algorithm #1, our first scene involves constant acceleration. So let’s pick a value.

    acceleration = new Vector2(-0.1f, -1f);
    

Maybe you’re thinking, “Gosh, those values seem awfully small!” That’s right, they are quite tiny. It’s important to realize that our acceleration values (measured in units) accumulate over time in the velocity, about thirty times per second depending on our scene’s frame rate. And so to keep the magnitude of the velocity vector within a reasonable range, our acceleration values should remain quite small. We can also help this cause by incorporating the Vector2 function ClampMagnitude().

    public class Mover
    {
        // The basic properties of a mover class
        private Vector2 location, velocity, acceleration;
        private float topSpeed;

        // The window limits
        private Vector2 maximumPos;

        // Gives the class a GameObject to draw on the screen
        private GameObject mover = GameObject.CreatePrimitive(PrimitiveType.Sphere);

        public Mover()
        {
            FindWindowLimits();

            // Vector2.zero is shorthand for a (0, 0) vector
            location = Vector2.zero;
            velocity = Vector2.zero;

            // Assign a random acceleration between -.1f and 1f
            acceleration = new Vector2(-0.1f, 1f);
            topSpeed = 10f;

            // We need to create a new material for WebGL
            Renderer r = mover.GetComponent<Renderer>();
            r.material = new Material(Shader.Find("Diffuse"));
        }

        public void Step()
        {
            // Speeds up the mover, Time.deltaTime is the time passed since the last frame and ties movement to a fixed rate instead of framerate
            velocity += acceleration * Time.deltaTime;

            // Limit Velocity to the top speed
            velocity = Vector2.ClampMagnitude(velocity, topSpeed);

            // Moves the mover
            location += velocity * Time.deltaTime;

            // Updates the GameObject of this movement
            mover.transform.position = new Vector2(location.x, location.y);
        }
    }
    

This translates to the following:

Example 1.8: Motion 101 (velocity and constant acceleration)

• Code
• Demo

Now on to Algorithm #2, a totally random acceleration. In this case, instead of initializing acceleration in the object’s constructor, we want to pick a new acceleration each cycle, i.e. each time update() is called.

Example 1.9: Motion 101 (velocity and random acceleration)

• Code
• Demo

Because the random vector is a normalized one, we can try scaling it:

    // Random acceleration but it's not normalized
    acceleration = new Vector2(Random.Range(-1f, 1f), Random.Range(-1f, 1f));

    // Normalize the acceletation
    acceleration.Normalize();

    // Now we can scale the magnitude as we wish
    acceleration *= Random.Range(5f, 10f);
    

While this may seem like an obvious point, it’s crucial to understand that acceleration does not merely refer to the speeding up or slowing down of a moving object, but rather any change in velocity in either magnitude or direction. Acceleration is used to steer an object, and we’ll see this again and again in future chapters as we begin to program objects that make decisions about how to move about the screen.

1.9 Static vs. Non-Static Functions

Before we get to Algorithm #3 (accelerate towards the mouse), we need to cover one more rather important aspect of working with vectors and the Vector2 class: the difference between using static methods and non-static methods.

    float x = 0;
    float y = 5;

    x = x + y;
    

Pretty simple, right? x has the value of 0, we add y to it, and now x is equal to 5. We could write the corresponding code pretty easily based on what we’ve learned about Vector2.

    Vector2 v = new Vector2(0,0);
    Vector2 u = new Vector2(4,5);
    

The vector v has the value of (0,0), we add u to it, and now v is equal to (4,5). Easy, right?

    float x = 0;
    float y = 5;

    float z = x + y;
    

x has the value of 0, we add y to it, and store the result in a new variable z. The value of x does not change in this example (neither does y)! This may seem like a trivial point, and one that is quite intuitive when it comes to mathematical operations with floats. However, it’s not so obvious with mathematical operations in Vector2. Let’s try to write the code based on what we know so far.

    Vector2 v = new Vector2(0,0);
    Vector2 u = new Vector2(4,5);
    Vector2 w = AddVectors(v, u);
    

The above might seem like a good guess, but it’s just not the way the Vector2 class works. If we look at one definition of AddVectors() . . .

    void AddVectors(Vector2 vectorA, Vector2 vectorB)
    {
        float newX = vectorA.x + vectorB.x;
        float newY = vectorA.y + vectorB.y;
    }
    

we see that this code does not accomplish our goal. First, it does not return a new Vector2 (the return type is “void”) and second, it changes the value of the Vector2 upon which it is called. In order to add two Vector2 objects together and return the result as a new Vector2, we must use the static AddVectors() function. Here is an example of the AddVectors() method returning a new Vector2.

Functions that we call from the class name itself (rather than from a specific object instance) are known as static functions. Here are two examples of function calls that assume two Vector2 objects, v and u:

    AddVectors(v,u);
    //Not static: called from an object instance.
    v.Add(u);
    

You might not have encountered static methods before. Vector2's static functions allow us to perform generic mathematical operations on Vector2 objects without having to adjust the value of one of the input Vector2s. Let’s look at how we might write the static version of Distance(Vector2 a, Vector2 b). It returns the distance between two vectors.

    public static float Distance(Vector2 a, Vector2 b);
    

There are several differences here:

• The function is labeled as static.
• The function does not have a void return type, but rather returns a Vector2.
• The function creates a new Vector2 (v3) and returns the sum of the components of v1 and v2 in that new Vector2.

When you call a static function, instead of referencing an actual object instance, you simply reference the name of the class itself.

    static Vector2 addVectors(Vector2 vectorA, Vector2 vectorB)
    {
        float newX = vectorA.x + vectorB.x;
        float newY = vectorA.y + vectorB.y;
        return new Vector2(newX, newY);
    }
    

The Vector2 class has static versions of Angle(), ClampMagnitude(), Reflect(), and more.

    Vector2 v = new Vector2(1,5);
    Vector2 u = ________._____(__,__);
    Vector2 w = ________._____(__,__);
    ___________;
    

1.10 Interactivity with Acceleration

To finish out this chapter, let’s try something a bit more complex and a great deal more useful. We’ll dynamically calculate an object’s acceleration according to a rule stated in Algorithm #3 — the object accelerates towards the mouse.

Figure 1.14

Anytime we want to calculate a vector based on a rule or a formula, we need to compute two things: magnitude and direction. Let’s start with direction. We know the acceleration vector should point from the object’s location towards the mouse location. Let’s say the object is located at the point (x,y) and the mouse at (mouseX,mouseY).

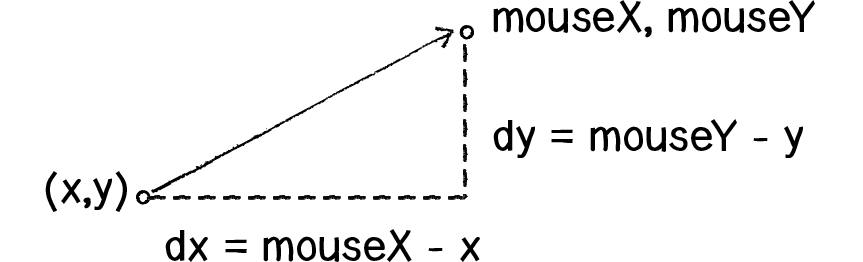
Figure 1.15

Let’s rewrite the above using Vector2 syntax. Assuming we are in the Mover class and thus have access to the object’s Vector2 position, we then have:

• dx = mouseX - x
• dy = mouseY - y

    Vector2 mousePos = Input.mousePosition;
    

We now have a Vector2 that points from the mover’s location all the way to the mouse. If the object were to actually accelerate using that vector, it would appear instantaneously at the mouse location. This does not make for good animation, of course, and what we want to do now is decide how quickly that object should accelerate toward the mouse.

    mover.SubtractVectors(mousePos, mover.location);
    

To summarize, we take the following steps:

• Calculate a vector that points from the object to the target location (mouse)
• Normalize that vector (reducing its length to 1)
• Scale that vector to an appropriate value (by multiplying it by some value)
• Assign that vector to acceleration

And here are those steps in the update() function itself:

Example 1.10: Accelerating towards the mouse

• Code
• Demo

You may be wondering why the circle doesn’t stop when it reaches the target. It’s important to note that the object moving has no knowledge about trying to stop at a destination; it only knows where the destination is and tries to go there as quickly as possible. Going as quickly as possible means it will inevitably overshoot the location and have to turn around, again going as quickly as possible towards the destination, overshooting it again, and so on and so forth. Stay tuned; in later chapters we’ll learn how to program an object to arrive at a location (slow down on approach).

This example is remarkably close to the concept of gravitational attraction (in which the object is attracted to the mouse location). Gravitational attraction will be covered in more detail in the next chapter. However, one thing missing here is that the strength of gravity (magnitude of acceleration) is inversely proportional to distance. This means that the closer the object is to the mouse, the faster it accelerates.

Let’s see what this example would look like with an array of movers (rather than just one).

Example 1.11: Array of movers accelerating towards the mouse

• Code
• Demo

Figure 1.16:

2. FORCES