Chapter 2. Forces
“Don’t underestimate the Force.”
— Darth VaderIn the final example of Chapter 1, we saw how we could calculate a dynamic acceleration based on a vector pointing from a circle on the screen to the mouse location. The resulting motion resembled a magnetic attraction between circle and mouse, as if some force were pulling the circle in towards the mouse. In this chapter we will formalize our understanding of the concept of a force and its relationship to acceleration. Our goal, by the end of this chapter, is to understand how to make multiple objects move around the screen and respond to a variety of environmental forces.
2.1 Forces and Newton’s Laws of Motion
Before we begin examining the practical realities of simulating forces in code, let’s take a conceptual look at what it means to be a force in the real world. Just like the word “vector,” “force” is often used to mean a variety of things. It can indicate a powerful intensity, as in “She pushed the boulder with great force” or “He spoke forcefully.” The definition of force that we care about is much more formal and comes from Isaac Newton’s laws of motion:
A force is a vector that causes an object with mass to accelerate.
The good news here is that we recognize the first part of the definition: a force is a vector. Thank goodness we just spent a whole chapter learning what a vector is and how to program with Vector2s!
Let’s look at Newton’s three laws of motion in relation to the concept of a force.
Newton’s First Law
Newton’s first law is commonly stated as:
An object at rest stays at rest and an object in motion stays in motion.
However, this is missing an important element related to forces. We could expand it by stating:
An object at rest stays at rest and an object in motion stays in motion at a constant speed and
direction unless acted upon by an unbalanced force.
By the time Newton came along, the prevailing theory of motion—formulated by Aristotle—was nearly two thousand years old. It stated that if an object is moving, some sort of force is required to keep it moving. Unless that moving thing is being pushed or pulled, it will simply slow down or stop. Right?
This, of course, is not true. In the absence of any forces, no force is required to keep an object moving. An object (such as a ball) tossed in the earth’s atmosphere slows down because of air resistance (a force). An object’s velocity will only remain constant in the absence of any forces or if the forces that act on it cancel each other out, i.e. the net force adds up to zero. This is often referred to as equilibrium. The falling ball will reach a terminal velocity (that stays constant) once the force of air resistance equals the force of gravity.
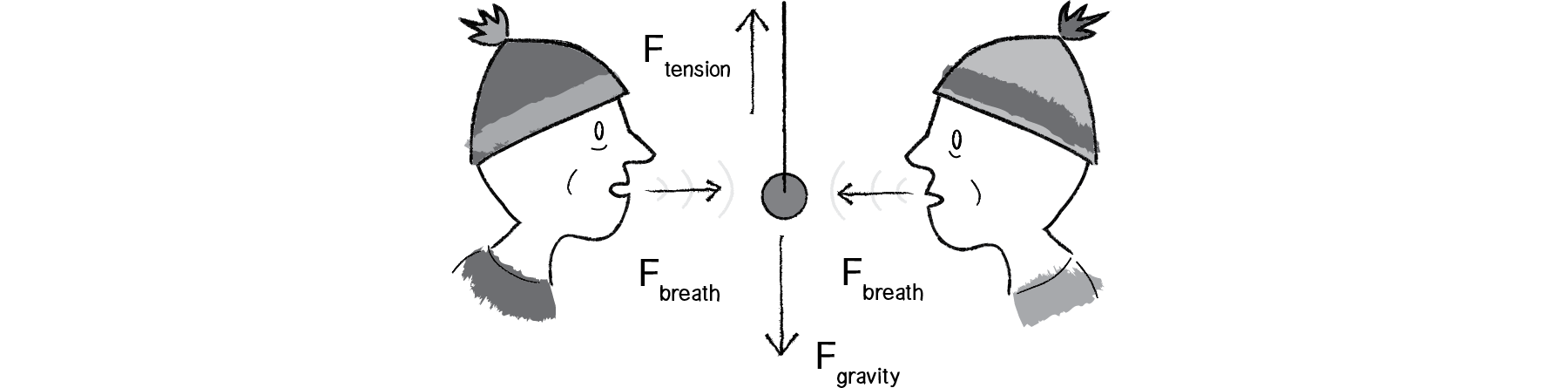
Figure 2.1: The pendulum doesn't move because all the forces cancel each other out (add up to a net force of zero).
In our Unity world, we could restate Newton’s first law as follows:
An object’s Vector2 velocity will remain constant if it is in a state of equilibrium.
Skipping Newton’s second law (arguably the most important law for our purposes) for a moment, let’s move on to the third law.
Newton’s Third Law
This law is often stated as:
For every action there is an equal and opposite reaction.
This law frequently causes some confusion in the way that it is stated. For one, it sounds like one force causes another. Yes, if you push someone, that someone may actively decide to push you back. But this is not the action and reaction we are talking about with Newton’s third law.
Let’s say you push against a wall. The wall doesn’t actively decide to push back on you. There is no “origin” force. Your push simply includes both forces, referred to as an “action/reaction pair.”
A better way of stating the law might be:
Forces always occur in pairs. The two forces are of equal strength, but in opposite directions.
Now, this still causes confusion because it sounds like these forces would always cancel each other out. This is not the case. Remember, the forces act on different objects. And just because the two forces are equal, it doesn’t mean that the movements are equal (or that the objects will stop moving).
Try pushing on a stationary truck. Although the truck is far more powerful than you, unlike a moving one, a stationary truck will never overpower you and send you flying backwards. The force you exert on it is equal and opposite to the force exerted on your hands. The outcome depends on a variety of other factors. If the truck is a small truck on an icy downhill, you’ll probably be able to get it to move. On the other hand, if it’s a very large truck on a dirt road and you push hard enough (maybe even take a running start), you could injure your hand.
And if you are wearing roller skates when you push on that truck?
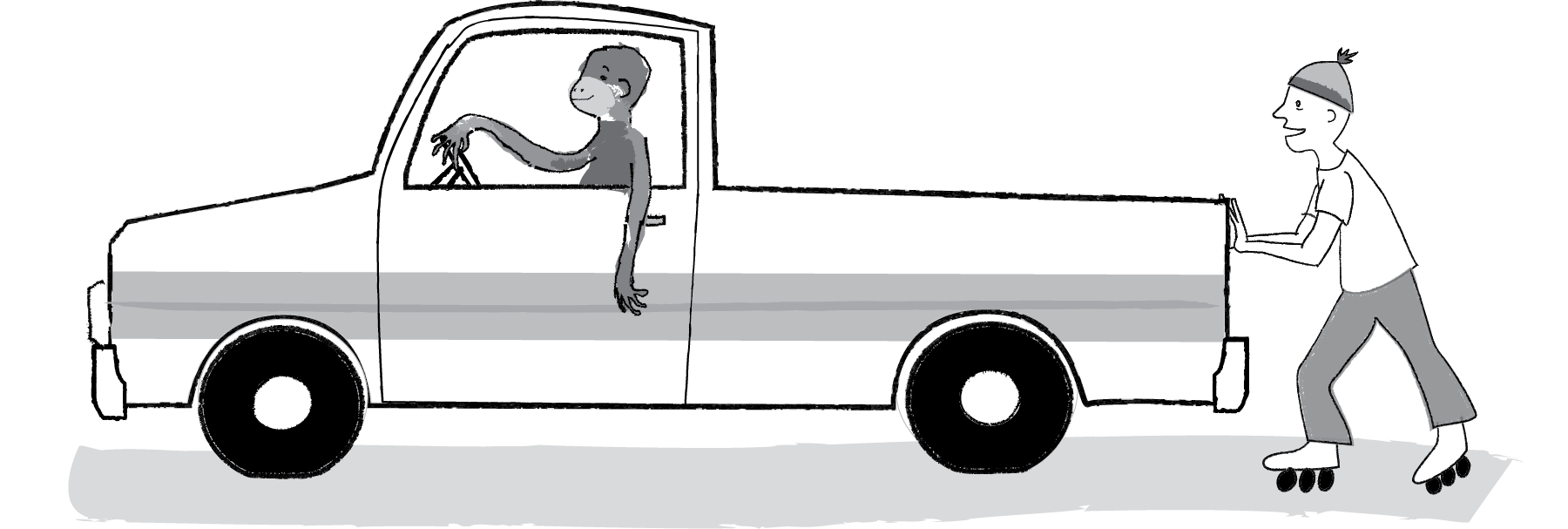
Figure 2.2
You’ll accelerate away from the truck, sliding along the road while the truck stays put. Why do you slide but not the truck? For one, the truck has a much larger mass (which we’ll get into with Newton’s second law). There are other forces at work too, namely the friction of the truck’s tires and your roller skates against the road.
Newton’s Third Law (as seen through the eyes of this Remix)
If we calculate a Vector2 f that is a force of object A on object B, we must also apply the
force that B exerts on object A.
We’ll see that in the world of Unity programming, we don’t always have to stay true to the above. Sometimes, such as in the case of see gravitational attraction between bodies, we’ll want to model equal and opposite forces. Other times, such as when we’re simply saying, “Hey, there’s some wind in the environment,” we’re not going to bother to model the force that a body exerts back on the air. In fact, we’re not modeling the air at all! Remember, we are simply taking inspiration from the physics of the natural world, not simulating everything with perfect precision.
2.2 Forces and this Remix—Newton’s Second Law as a Function
And here we are at the most important law for this section.
Newton’s Second Law
This law is stated as:
Force equals mass times acceleration.
Or:
Why is this the most important law for us? Well, let’s write it a different way.
Acceleration is directly proportional to force and inversely proportional to mass. This means that if you get pushed, the harder you are pushed, the faster you’ll move (accelerate). The bigger you are, the slower you’ll move.
Weight vs. Mass
- The mass of an object is a measure of the amount of matter in the object (measured in kilograms).
- Weight, though often mistaken for mass, is technically the force of gravity on an object. From Newton’s second law, we can calculate it as mass times the acceleration of gravity (w = m * g). Weight is measured in newtons.
- Density is defined as the amount of mass per unit of volume (grams per cubic centimeter, for example).
Note that an object that has a mass of one kilogram on earth would have a mass of one kilogram on the moon. However, it would weigh only one-sixth as much.
Now, in the world of this Remix, what is mass anyway? Aren’t we dealing with pixels? To start in a simpler place, let’s say that in our pretend pixel world, all of our objects have a mass equal to 1. F/ 1 = F. And so:
The acceleration of an object is equal to force. This is great news. After all, we saw in Chapter 1 that acceleration was the key to controlling the movement of our objects on screen. Location is adjusted by velocity, and velocity by acceleration. Acceleration was where it all began. Now we learn that force is truly where it all begins.
Let’s take our Mover class, with location, velocity, and acceleration.
public class Mover
{
// The basic properties of a mover class
public Vector2 location, velocity, acceleration;
}
Now our goal is to be able to add forces to this object, perhaps saying:
// ForceMode.Impulse takes mass into account
mover.body.AddForce(wind, ForceMode.Impulse);
or:
mover.body.AddForce(gravity, ForceMode.Impulse);
where wind and gravity are Vector2s. According to Newton’s second law, we could implement this function that is part of Unity's Rigidbody component. as follows.
// body is the Rigidbody component. We apply forces to that Ridigbody.
someGameObject.body.AddForce(force, ForceMode.Impulse)
// The application of Vector2 force in this instance can be understood as
acceleration = force
// Which we can handle through the Rigidbody component
// Use Acceleration as the force on the Rigidbody
// As both are Vector2s
someGameObject.body.AddForce(m_NewForce, ForceMode.Acceleration);
A Rigidbody gives us control of an object's position through physics simulation. Adding a Rigidbody component to an object will put its motion under the control of Unity's physics engine. Even without adding any code, a Rigidbody object will be pulled downward by gravity.
The Rigidbody also has a scripting API that lets you apply forces to the object and control it in a physically realistic way. For example, a car's behaviour can be specified in terms of the forces applied by the wheels. Given this information, the physics engine can handle most other aspects of the car's motion, so it will accelerate realistically and respond correctly to collisions.
A common problem when starting out with Rigidbodies is that the game physics appears to run in "slow motion". This is actually due to the scale used for your models. The default gravity settings assume that one world unit corresponds to one metre of distance. With non-physical games, it doesn't make much difference if your models are all 100 units long but when using physics, they will be treated as very large objects. If a large scale is used for objects that are supposed to be small, they will appear to fall very slowly - the physics engine thinks they are very large objects falling over very large distances. With this in mind, be sure to keep your objects more or less at their scale in real life (so a car should be about 4 units = 4 metres, for example).
2.3 Force Accumulation
This looks pretty good. After all, acceleration = force is a literal translation of Newton’s second law (without mass). Nevertheless, there’s a pretty big problem here. Let’s return to what we are trying to accomplish: creating a moving object on the screen that responds to wind and gravity.
mover.body.AddForce(wind, ForceMode.Impulse);
// Unity give us a few options for how we apply force. Impulse does it as a burst. This makes it great for wind.
// ForceMode.Force, allows us to add a continuous force like gravity.
mover.body.AddForce(gravity, ForceMode.Force);
Ok, let’s be the computer for a moment. First, we call the Rigidybody's AddForce() with wind. And so the Mover object’s acceleration is now assigned the Vector2 wind. Second, we call AddForce() with gravity. Now the Mover object’s acceleration is set to the gravity Vector2. Third, we call update(). What happens in update()? Acceleration is added to velocity.
Acceleration is equal to the sum of all forces divided by mass. That is why we can AddForce() with both gravity and wind and they don't cancel one another out. This makes perfect sense. After all, as we saw in Newton’s first law, if all the forces add up to zero, an object experiences an equilibrium state (i.e. no acceleration). Our implementation of this is through a process known as force accumulation. It’s actually very simple; all we need to do is add all of the forces together. At any given moment, there might be 1, 2, 6, 12, or 303 forces. As long as our object knows how to accumulate them, it doesn’t matter how many forces act on it.
Now, we’re not finished just yet. Force accumulation has one more piece. Since we’re adding all the forces together at any given moment, we have to make sure that we clear acceleration (i.e. set it to zero) before each time update() is called. Let’s think about wind for a moment. Sometimes the wind is very strong, sometimes it’s weak, and sometimes there’s no wind at all. At any given moment, there might be a huge gust of wind, say, when the user holds down the mouse.
if (Input.GetMouseButtonDown(0))
{
Vector2 wind = new Vector2(0,1,0);
mover.body.AddForce(wind, ForceMode.Impulse);
}
When the user releases the mouse, the wind will stop, and according to Newton’s first law, the object will continue to move at a constant velocity.
Exercise 2.1
Using forces, simulate a helium-filled balloon floating upward and bouncing off the top of a window. Can you add a wind force that changes over time, perhaps according to Perlin noise?
2.4 Forces and Newton’s Laws of Motion
OK. We’ve got one tiny little addition to make before we are done with integrating forces into our Mover class and are ready to look at examples. After all, Newton’s second law is really F→=M×A→, not A→=F→. Incorporating mass is as it is part of the RigidBody component.
First we need to add mass and take into account the volume of the GameObject.
public class Mover
{
// The basic properties of a mover class
public Vector2 location, velocity, acceleration;
// Add the Rigidbody to apply forces, give this object mass, and more physics galore.
public Rigidbody body;
// We need to calculate the mass of the sphere.
// Assuming the sphere is of even density throughout,
// The mass will be proportional to the volume.
body.mass = (4f / 3f) * Mathf.PI * radius * radius * radius;
}
Units of Measurement
Now that we are introducing mass, it’s important to make a quick note about units of measurement. In the real world, things are measured in specific units. We say that two objects are 3 meters apart, the baseball is moving at a rate of 90 miles per hour, or this bowling ball has a mass of 6 kilograms. As we’ll see later in this book, sometimes we will want to take real-world units into consideration. However, in this chapter, we’re going to ignore them for the most part. Our units of measurement are in meters (“These two circles are 100 meters apart”) and frames of animation (“This circle is moving at a rate of 2 pixels per frame”). In the case of mass, there isn’t any unit of measurement for us to use. We’re just going to make something up. In this example, we’re arbitrarily picking the number 10. There is no unit of measurement, though you might enjoy inventing a unit of your own, like “1 moog” or “1 yurkle.” It should also be noted that, for demonstration purposes, we’ll tie mass to pixels (drawing, say, a circle with a radius of 10). This will allow us to visualize the mass of an object. In the real world, however, size does not definitely indicate mass. A small metal ball could have a much higher mass than a large balloon due to its higher density.
Mass is a scalar (float), not a vector, as it’s just one number describing the amount of matter in an object. We could be fancy about things and compute the area of a shape as its mass, but it’s simpler to begin by saying, “Hey, the mass of this object is…um, I dunno…how about 10?”
public class Mover
{
// The basic properties of a mover class
public Vector2 location = Vector2.zero;
public Vector2 velocity = Vector2.zero;
public Vector2 acceleration = Vector2.zero;
// Add the Rigidbody to apply forces, give this object mass, and more physics galore.
public Rigidbody body;
// We would usually calculate the mass of the sphere.
// Assuming the sphere is of even density throughout,
// The mass will be proportional to the volume. This time, we are just making it 10.
body.mass = 10f;
}
This isn’t so great since things only become interesting once we have objects with varying mass, but it’ll get us started. Where does mass come in? We use it while applying Newton’s second law to our object. In fact, this is exactly what ForceMode handles. ForceMode allows you to choose four different ways to affect the GameObject using this Force: Acceleration, Force, Impulse, and VelocityChange. We already discussed Accelertion mode, which allows us to use the object's acceleration as its force. Another is Impulse mode, which involves using the Rigidbody’s mass to apply an instant impulse force. ForceMode.Force, uses a continuous force on the Rigidbody considering its mass. VelocityChange ignores mass and so we will be ignoring it. Gravity would be continuous and so use ForceMode.Force where as wind would be an impulse and use ForceMode.Impulse.
//A continuous force that takes mass into account
body.AddForce(gravity, ForceMode.Force);
//An impulse, burst force that takes mass into account
body.AddForce(wind, ForceMode.Impulse);
2.5 Creating Forces
Let’s take a moment to remind ourselves where we are. We know what a force is (a vector), and we know how to apply a force to an object (divide it by mass and add it to the object’s acceleration vector). What are we missing? Well, we have yet to figure out how we get a force in the first place. Where do forces come from?
In this chapter, we’ll look at two methods for creating forces in our Unity world.
- Make up a force! After all, you are the programmer, the creator of your world. There’s no reason why you can’t just make up a force and apply it.
- Model a force! Yes, forces exist in the real world. And physics textbooks often contain formulas for these forces. We can take these formulas, translate them into source code, and model real-world forces in Unity.
The easiest way to make up a force is to just pick a number. Let’s start with the idea of simulating wind. How about a wind force that points to the right and is fairly weak? Assuming a Mover object mover, our code would look like:
Vector2 wind = new Vector2(0,1);
mover.body.AddForce(wind, ForceMode.Impulse);
The result isn’t terribly interesting, but it is a good place to start. We create a Vector2 object, initialize it, and pass it into an object (which in turn will apply it to its own acceleration). If we wanted to have two forces, perhaps wind and gravity (a bit stronger, pointing down), we might write the following:
Example 2.1: Forces
Now we have two forces, pointing in different directions with different magnitudes, both applied to object mover. We’re beginning to get somewhere. We’ve now built a world for our objects in the Unity Remix, an environment to which they can actually respond.
Let’s look at how we could make this example a bit more exciting with many objects of varying mass. To do this, we’ll need a quick review of object-oriented programming. Again, we’re not covering all the basics of programming here (for that you can check out any of the intro Untity books listed in the introduction). However, since the idea of creating a world filled with objects is pretty fundamental to all the examples in this book, it’s worth taking a moment to walk through the steps of going from one object to many.
This is where we are with the Mover class as a whole. Notice how it is identical to the Mover class created in Chapter 1, with additions--the Rigidbody component and its ability to use AddForce().
public class Mover2_1
{
public Rigidbody body;
private GameObject gameObject;
private float radius;
private float xMin;
private float xMax;
private float yMin;
public Mover2_1(Vector3 position, float xMin, float xMax, float yMin)
{
this.xMin = xMin;
this.xMax = xMax;
this.yMin = yMin;
// Initialize the components required for the mover
gameObject = GameObject.CreatePrimitive(PrimitiveType.Sphere);
body = gameObject.AddComponent<Rigidbody>();
// Remove functionality that come with the primitive that we don't want
// Destroy() is a built in Unity function that removes a GameObject
gameObject.GetComponent<SphereCollider>().enabled = false;
Object.Destroy(gameObject.GetComponent<SphereCollider>());
// Generate a radius of 1f for this mover
radius = 1f;
// Place our mover at the specified spawn position relative
// to the bottom of the sphere
gameObject.transform.position = position + Vector3.up * radius;
// The default diameter of the sphere is one unit
// This means we have to multiple the radius by two when scaling it up
gameObject.transform.localScale = 2 * radius * Vector3.one;
// We need to calculate the mass of the sphere.
// Assuming the sphere is of even density throughout,
// the mass will be proportional to the volume.
body.mass = (4f / 3f) * Mathf.PI * (radius * radius * radius);
}
// Checks to ensure the body stays within the boundaries
public void CheckEdges()
{
Vector3 restrainedVelocity = body.velocity;
if (body.position.y - radius < yMin)
{
// Using the absolute value here is an important safe
// guard for the scenario that it takes multiple ticks
// of FixedUpdate for the mover to return to its boundaries.
// The intuitive solution of flipping the velocity may result
// in the mover not returning to the boundaries and flipping
// direction on every tick.
restrainedVelocity.y = Mathf.Abs(restrainedVelocity.y);
body.position = new Vector3(body.position.x, yMin, body.position.z) + Vector3.up * radius;
}
if (body.position.x - radius < xMin)
{
restrainedVelocity.x = Mathf.Abs(restrainedVelocity.x);
body.position = new Vector3(xMin, body.position.y, body.position.z) + Vector3.right * radius;
}
else if (body.position.x + radius > xMax)
{
restrainedVelocity.x = -Mathf.Abs(restrainedVelocity.x);
body.position = new Vector3(xMax, body.position.y, body.position.z) + Vector3.left * radius;
}
body.velocity = restrainedVelocity;
}
}
Now that our class is set, we can choose to create, say, thirty Mover objects with a List.
// Create a list of movers
private List<Mover2_2> movers = new List<Mover2_2>();
// Start is called before the first frame update
void Start()
{
// Create copys of our mover and add them to our list
while (movers.Count < 30)
{
// Instantiate the mover and add it to our list. Pass in the spawn location, x bounds of the walls and the y location of the floor
movers.Add(new Mover2_2(moverSpawnTransform.position,leftWallX,rightWallX,floorY));
}
}
We can create a variety of Mover objects: big ones, small ones, ones that start on the left side of the screen, ones that start on the right, etc.
For each mover created, the mass is set to a random value between 0.1 and .4. Certainly, there are all sorts of ways we might choose to initialize the objects; this is just a demonstration of one possibility.
// Generate random properties for this mover
radius = Random.Range(0.1f, 0.4f);
// Generate a random x value within the bundaries
xSpawn = Random.Range(xMin, xMax);
// Place our mover at a randomized spawn position relative
// to the bottom of the sphere
gameObject.transform.position = new Vector3(xSpawn, position.y, position.z) + Vector3.up * radius;
// The default diameter of the sphere is one unit
// This means we have to multiple the radius by two when scaling it up
gameObject.transform.localScale = 2 * radius * Vector3.one;
// We need to calculate the mass of the sphere.
// Assuming the sphere is of even density throughout,
// the mass will be proportional to the volume.
body.mass = (4f / 3f) * Mathf.PI * (radius * radius * radius);
Once the list of objects is declared, created, and initialized, the rest of the code is simple. We run through every object, hand them each the forces in the environment, and enjoy the show.
// Update is called once per frame
void FixedUpdate()
{
// Apply the forces to each of the Movers
foreach (Mover2_2 mover in movers)
{
// ForceMode.Impulse and Forcemode.Force take mass into account
mover.body.AddForce(wind, ForceMode.Impulse);
mover.body.AddForce(gravity, ForceMode.Force);
mover.CheckEdges();
}
}
Example 2.2: Forces Acting on Many Objects
Note how in the above image, the smaller circles reach the right of the window faster than the larger ones. This is because of our formula: acceleration = force divided by mass. The larger the mass, the smaller the acceleration.
Exercise 2.2
Create create an example where the Ridigbody's mass is dyanmic.
Exercise 2.3
Instead of objects bouncing off the edge of the wall, create an example in which an invisible force pushes back on the objects to keep them in the window. Can you weight the force according to how far the object is from an edge—i.e., the closer it is, the stronger the force?
2.6 Gravity on Earth and Modeling a Force
If you were to climb to the top of the Leaning Tower of Pisa and drop two balls of different masses, which one will hit the ground first? According to legend, Galileo performed this exact test in 1589, discovering that they fell with the same acceleration, hitting the ground at the same time. Why is this? The force of gravity is calculated relative to an object’s mass. The bigger the object, the stronger the force. So if the force is scaled according to mass, it is canceled out when acceleration is divided by mass. We can implement this in our scene rather easily by using the Rigidbody's gravity, which can be modified in Unity's settings, or by creating our own gravity Vector2 force and using body.AddForce(gravity, ForceMode.Force); In this example, we use the built in Unity gravity.
Example 2.3: Gravity scaled by mass
While the objects now fall at the same rate, because the strength of the wind force is dependent upon mass, the smaller objects still accelerate to the right more quickly.
Making up forces will actually get us quite far. The world of Unity is a pretend world and you are its master. So whatever you deem appropriate to be a force, well by golly, that’s the force it should be. Nevertheless, there may come a time where you find yourself wondering: “But how does it really all work?”
Open up any high school physics textbook and you will find some diagrams and formulas describing many different forces—gravity, electromagnetism, friction, tension, elasticity, and more. In this chapter we’re going to look at two forces—friction and gravity. The point we’re making here is not that friction and gravity are fundamental forces that you always need to have in your Unity scenes. Rather, we want to evaluate these two forces as case studies for the following process:
- Understanding the concept behind a force
- Deconstructing the force’s formula into two parts:
- How do we compute the force’s direction?
- How do we compute the force’s magnitude?
- Translating that formula into Unity code that calculates a Vector2 to be sent through our Mover's AddForce() function
If we can follow the above steps with two forces, then hopefully if you ever find yourself Googling “atomic nuclei weak nuclear force” at 3 a.m., you will have the skills to take what you find and adapt it for Unity.
2.7 Friction
Let’s begin with friction and follow our steps.
Friction is a dissipative force. A dissipative force is one in which the total energy of a system decreases when an object is in motion. Let’s say you are driving a car. When you press your foot down on the brake pedal, the car’s brakes use friction to slow down the motion of the tires. Kinetic energy (motion) is converted into thermal energy (heat). Whenever two surfaces come into contact, they experience friction. A complete model of friction would include separate cases for static friction (a body at rest against a surface) and kinetic friction (a body in motion against a surface), but for our purposes, we are only going to look at the kinetic case.
Here’s the formula for friction:
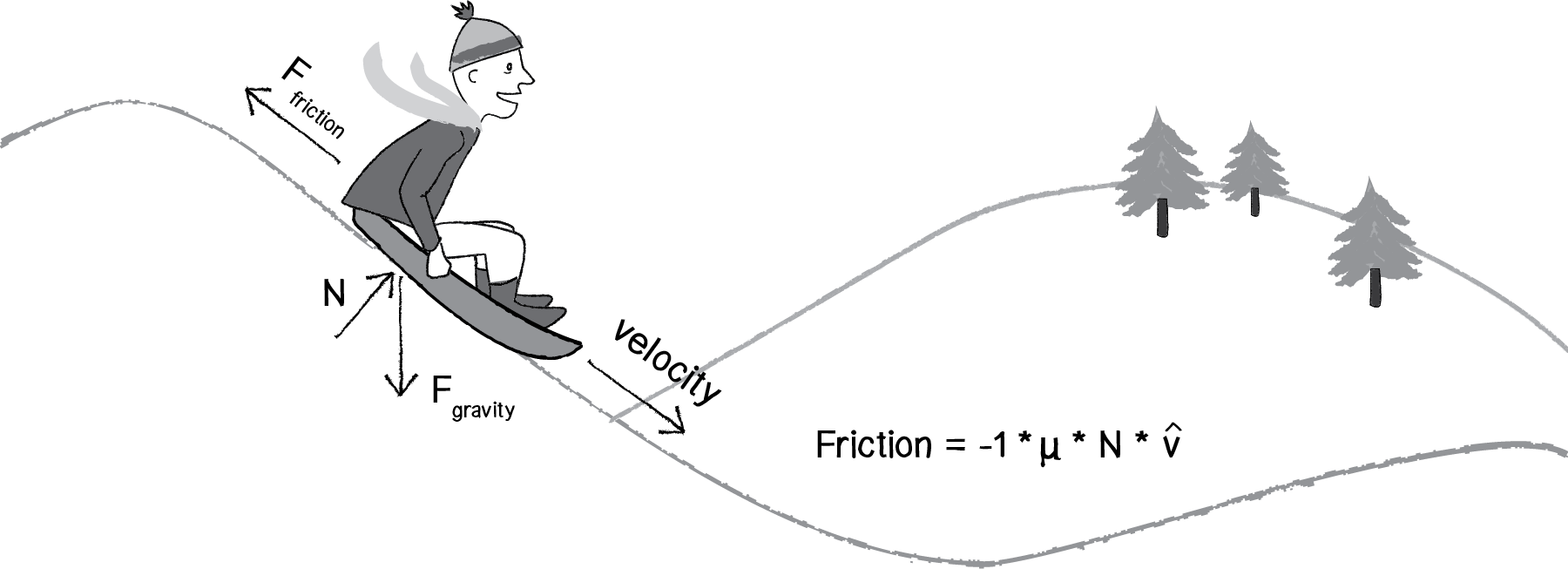
Figure 2.3: The formula for friction.
It’s now up to us to separate this formula into two components that determine the direction of friction as well as the magnitude. Based on the diagram above, we can see that friction points in the opposite direction of velocity. In fact, that’s the part of the formula that says -1 * v∧, or -1 times the velocity unit vector. This would mean taking the velocity vector, normalizing it, and multiplying by -1.
// Define an arbitrary friction strength
private float frictionStrength = 0.5f;
// Update is called once per frame
void FixedUpdate()
{
// Apply the forces to each of the Movers
foreach (Mover2_4 mover in movers)
{
// Apply a friction force that directly opposes the current motion
Vector3 friction = -mover.body.velocity;
friction.Normalize();
friction *= frictionStrength;
mover.body.AddForce(friction, ForceMode.Force);
}
}
Notice two additional steps here. First, it’s important to make a copy of the velocity vector, as we don’t want to reverse the object’s direction by accident. Second, we normalize the vector. This is because the magnitude of friction is not associated with how fast it is moving, and we want to start with a friction vector of magnitude 1 so that it can easily be scaled.
According to the formula, the magnitude is μ * N. μ, the Greek letter mu (pronounced “mew”), is used here to describe the coefficient of friction. The coefficient of friction establishes the strength of a friction force for a particular surface. The higher it is, the stronger the friction; the lower, the weaker. A block of ice, for example, will have a much lower coefficient of friction than, say, sandpaper. Since we’re in a pretend Unity world, we can arbitrarily set the coefficient based on how much friction we want to simulate.
// Define an arbitrary friction strength
private float frictionStrength = 0.5f;
Now for the second part: N. N refers to the normal force, the force perpendicular to the object’s motion along a surface. Think of a vehicle driving along a road. The vehicle pushes down against the road with gravity, and Newton’s third law tells us that the road in turn pushes back against the vehicle. That’s the normal force. The greater the gravitational force, the greater the normal force. As we’ll see in the next section, gravity is associated with mass, and so a lightweight sports car would experience less friction than a massive tractor trailer truck. With the diagram above, however, where the object is moving along a surface at an angle, computing the normal force is a bit more complicated because it doesn’t point in the same direction as gravity. We’ll need to know something about angles and trigonometry.
All of these specifics are important; however, in Unity, a “good enough” simulation can be achieved without them. We can, for example, make friction work with the assumption that the normal force will always have a magnitude of 1. When we get into trigonometry in the next chapter, we’ll remember to return to this question and make our friction example a bit more sophisticated. Therefore:
friction.Normalize();
Now that we have both the magnitude and direction for friction, we can put it all together…
// ForceMode.Impulse takes mass into account
mover.body.AddForce(wind, ForceMode.Impulse);
// Apply a friction force that directly opposes the current motion
Vector3 friction = -mover.body.velocity;
friction.Normalize();
friction *= frictionStrength;
mover.body.AddForce(friction, ForceMode.Force);
…and add it to our “forces” example, where many objects experience wind, gravity, and now friction:
 An example where mass is not taken into account when computing friction.
An example where mass is not taken into account when computing friction.
 An example where mass is taken into account when computing friction.
An example where mass is taken into account when computing friction.
Example 2.4: Including Friction
Running this example, you’ll notice that the circles don’t even make it to the right side of the window. Since friction continuously pushes against the object in the opposite direction of its movement, the object continuously slows down. This can be a useful technique or a problem depending on the goals of your visualization.
Exercise 2.4
Create pockets of friction in a Unity Scene so that objects only experience friction when crossing over those pockets. What if you vary the strength (friction coefficient) of each area? What if you make some pockets feature the opposite of friction—i.e., when you enter a given pocket you actually speed up instead of slowing down?
2.8 Air and Fluid Resistance

Figure 2.4
Friction also occurs when a body passes through a fluid or gas. This force has many different names, all really meaning the same thing: viscous force, drag force, fluid resistance. While the result is ultimately the same as our previous friction examples (the object slows down), the way in which we calculate a drag force will be slightly different. Let’s look at the formula:
Let’s implement this force in our Mover class example with one addition. When we wrote our friction example, the force of friction was always present. Whenever an object was moving, friction would slow it down. Here, let’s introduce an element to the environment—a “fluid” that the Mover objects pass through. The fluid object will be a rectangle and will know about its location, width, height, and “coefficient of drag”—i.e., is it easy for objects to move through it (like air) or difficult (like molasses)? In addition, it should include a function to draw itself on the screen (and two more functions, which we’ll see in a moment).
Now comes an interesting question: how do we get the Mover object to talk to the fluid object? In other words, we want to execute the following:
When a mover passes through a fluid it experiences a drag force.
…or in object-oriented speak (assuming we are looping through an array of Mover objects with index i):
// Create our lists
private List<Mover2_5> movers = new List<Mover2_5>();
private List<Fluid2_5> fluids = new List<Fluid2_5>();
// Start is called before the first frame update
void Start()
{
// Create copys of our mover and add them to our list
while (movers.Count < 30)
{
movers.Add(new Mover2_5(moverSpawnTransform.position,leftWallX,rightWallX,floorY));
}
// Add the fluid to our scene
fluids.Add(new Fluid2_5(fluidCornerA.position,fluidCornerB.position,fluidDrag,waterMaterial));
}
// Update is called once per frame
void FixedUpdate()
{
// Apply the forces to each of the Movers
foreach (Mover2_5 mover in movers)
{
// Check for interaction with any of our fluids
foreach(Fluid2_5 fluid in fluids)
{
if(mover.IsInside(fluid))
{
// Apply a friction force that directly opposes the current motion
Vector3 friction = -mover.body.velocity;
friction.Normalize();
friction *= fluid.dragCoefficient;
mover.body.AddForce(friction, ForceMode.Force);
}
}
mover.CheckEdges();
}
}
The above code tells us that we need to add two functions to the Mover class: (1) a function that determines if a Mover object is inside the Fluid object, and (2) a function or property that computes and applies a drag force on the Mover object.
The first is easy; we can simply use a conditional statement to determine if the location vector rests inside the rectangle defined by the fluid.
As a note, the Rigidbody component has a drag property that you can access.
if(mover.IsInside(fluid))
{
// Apply a friction force that directly opposes the current motion
Vector3 friction = -mover.body.velocity;
friction.Normalize();
friction *= fluid.dragCoefficient;
mover.body.AddForce(friction, ForceMode.Force);
}
The dragCoefficient property is a bit more complicated; however, we’ve written the code for it already. This is simply an implementation of our formula. The drag force is equal to the coefficient of drag multiplied by the speed of the Mover squared in the opposite direction of velocity! This is what is occurring above. However, we need to set the dragCoefficient in the Fluid2_5 class. We can always set this in the inspector.
public class Fluid2_5
{
public Vector3 minBoundary;
public Vector3 maxBoundary;
public float dragCoefficient;
public Fluid2_5(Vector3 corner1, Vector3 corner2, float dragCoefficient, Material material)
{
// Get the minimum and maximum corners of the rectangular prism
// This code allows the designer to place the volume corners at
// any of the eight possible diagonals of a rectangular prism.
minBoundary = new Vector3(
Mathf.Min(corner1.x, corner2.x),
Mathf.Min(corner1.y, corner2.y),
Mathf.Min(corner1.z, corner2.z)
);
maxBoundary = new Vector3(
Mathf.Max(corner1.x, corner2.x),
Mathf.Max(corner1.y, corner2.y),
Mathf.Max(corner1.z, corner2.z)
);
this.dragCoefficient = dragCoefficient;
// Create the presence of the object in 3D space
GameObject obj = GameObject.CreatePrimitive(PrimitiveType.Cube);
obj.GetComponent<Renderer>().material = material;
// Remove undesired components that come with the primitive
obj.GetComponent<BoxCollider>().enabled = false;
Object.Destroy(obj.GetComponent<BoxCollider>());
// Position and scale the new cube to match the boundaries.
obj.transform.position = (corner1 + corner2) / 2;
obj.transform.localScale = new Vector3(
Mathf.Abs(corner2.x - corner1.x),
Mathf.Abs(corner2.y - corner1.y),
Mathf.Abs(corner2.z - corner1.z)
);
}
}
Finally, we have to implement our method to check if the mover is inside the fluid.
public bool IsInside(Fluid2_5 fluid)
{
// Check to see if the mover is inside the range on each axis.
if (body.position.x > fluid.minBoundary.x &&
body.position.x < fluid.maxBoundary.x &&
body.position.y > fluid.minBoundary.y &&
body.position.y < fluid.maxBoundary.y &&
body.position.z > fluid.minBoundary.z &&
body.position.z < fluid.maxBoundary.z)
{
return true;
}
else
{
return false;
}
}
And with these two properties added to the Mover class, we’re ready to put it all together in the main tab:
Example 2.5: Fluid Resistance
Running the example, you should notice that we are simulating balls falling into water. The objects only slow down when crossing through the gray area at the bottom of the window (representing the fluid). You’ll also notice that the smaller objects slow down a great deal more than the larger objects. Remember Newton’s second law? A = F / M. Acceleration equals force divided by mass. A massive object will accelerate less. A smaller object will accelerate more. In this case, the acceleration we’re talking about is the “slowing down” due to drag. The smaller objects will slow down at a greater rate than the larger ones.
Exercise 2.5
Take a look at our formula for drag again: drag force = coefficient * speed * speed. The faster an object moves, the greater the drag force against it. In fact, an object not moving in water experiences no drag at all. Expand the example to drop the balls from different heights. How does this affect the drag as they hit the water?
Exercise 2.6
The formula for drag also included surface area. Can you create a simulation of boxes falling into water with a drag force dependent on the length of the side hitting the water?
Exercise 2.7
Fluid resistance does not only work opposite to the velocity vector, but also perpendicular to it. This is known as “lift-induced drag” and will cause an airplane with an angled wing to rise in altitude. Try creating a simulation of lift.
2.9 Gravitational Attraction
Probably the most famous force of all is gravity. We humans on earth think of gravity as an apple hitting Isaac Newton on the head. Gravity means that stuff falls down. But this is only our experience of gravity. In truth, just as the earth pulls the apple towards it due to a gravitational force, the apple pulls the earth as well. The thing is, the earth is just so freaking big that it overwhelms all the other gravity interactions. Every object with mass exerts a gravitational force on every other object. And there is a formula for calculating the strengths of these forces, as depicted in Figure 2.6.
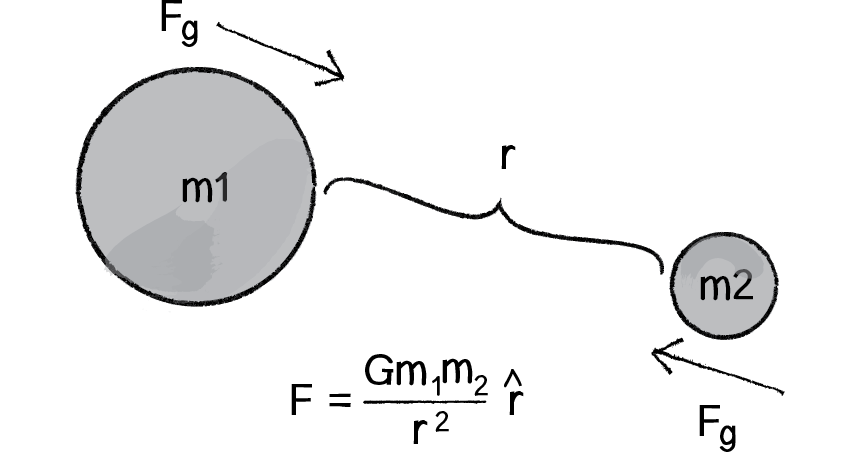
Figure 2.6
Let’s examine this formula a bit more closely.
- F refers to the gravitational force, the vector we ultimately want to compute and pass into our AddForce() function.
- G is the universal gravitational constant, which in our world equals 6.67428 x 10-11 meters cubed per kilogram per second squared. This is a pretty important number if your name is Isaac Newton or Albert Einstein. It’s not an important number if you are a C# programmer. Again, it’s a constant that we can use to make the forces in our world weaker or stronger. Just making it equal to one and ignoring it isn’t such a terrible choice either.
- m1 and m2 are the masses of objects 1 and 2. As we saw with Newton’s second law (F→=M×A→), mass is also something we could choose to ignore. After all, shapes drawn on the screen don’t actually have a physical mass. However, if we keep these values, we can create more interesting simulations in which “bigger” objects exert a stronger gravitational force than smaller ones.
- r∧ refers to the unit vector pointing from object 1 to object 2. As we’ll see in a moment, we can compute this direction vector by subtracting the location of one object from the other.
- r2 refers to the distance between the two objects squared. Let’s take a moment to think about this a bit more. With everything on the top of the formula—G, m1, m2—the bigger its value, the stronger the force. Big mass, big force. Big G, big force. Now, when we divide by something, we have the opposite. The strength of the force is inversely proportional to the distance squared. The farther away an object is, the weaker the force; the closer, the stronger.
Hopefully by now the formula makes some sense to us. We’ve looked at a diagram and dissected the individual components of the formula. Now it’s time to figure out how we translate the math into C# code. Let’s make the following assumptions.
- Each object has a location: Vector2 location1 and Vector2 location2.
- Each object has a mass: float mass1 and float mass2.
- There is a variable float G for the universal gravitational constant.
Given these assumptions, we want to compute Vector2 force, the force of gravity. We’ll do it in two parts. First, we’ll compute the direction of the force r∧ in the formula above. Second, we’ll calculate the strength of the force according to the masses and distance.
Remember in Chapter 1, when we figured out how to have an object accelerate towards the mouse? (See Figure 2.7.)
Figure 2.7
A vector is the difference between two points. To make a vector that points from the circle to the mouse, we simply subtract one point from another:
Vector2 dir = Input.mousePosition - location;
In our case, the direction of the attraction force that object 1 exerts on object 2 is equal to:
Vector2 dir = location1 - location2;
dir.Normalize();
Don’t forget that since we want a unit vector, a vector that tells us about direction only, we’ll need to normalize the vector after subtracting the locations.
OK, we’ve got the direction of the force. Now we just need to compute the magnitude and scale the vector accordingly.
float m = (G * mass1 * mass2) / (distance * distance);
dir *= m;
The only problem is that we don’t know the distance. G, mass1, and mass2 were all givens, but we’ll need to actually compute distance before the above code will work. Didn’t we just make a vector that points all the way from one location to another? Wouldn’t the length of that vector be the distance between two objects?
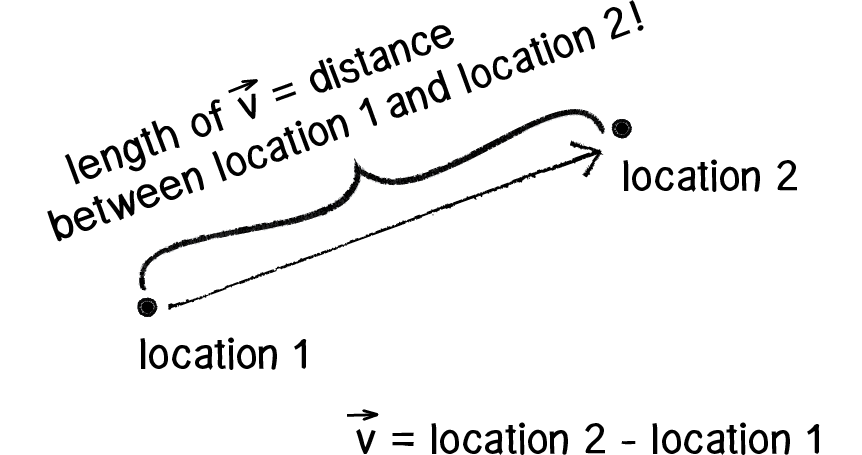
Figure 2.8
Well, if we add just one line of code and grab the magnitude of that vector before normalizing it, then we’ll have the distance.
Vector2 force = location1 - location2;
float distance = force.magnitude;
force.Normalize();
float m = (G * mass1 * mass2) / (distance * distance);
force *= m;
Note that I also renamed the Vector2 “dir” as “force.” After all, when we’re finished with the calculations, the Vector2 we started with ends up being the actual force vector we wanted all along.
Now that we’ve worked out the math and the code for calculating an attractive force (emulating gravity), we need to turn our attention to applying this technique in the context of an actual Unity scene. In Example 2.1, you may recall how we created a simple Mover object—a class with Vector2's location, velocity, and acceleration as well as an AddForce(). Let’s take this exact class and put it in a scene with:
- A single Mover object.
- A single Attractor object (a new class that will have a fixed location).
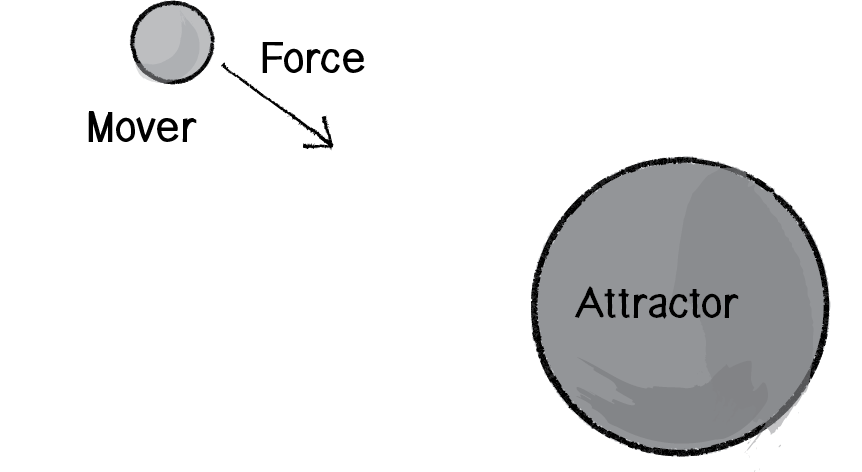
Figure 2.9
The Mover object will experience a gravitational pull towards the Attractor object, as illustrated in Figure 2.9.
We can start by making the new Attractor class very simple—giving it a location and a mass, along with a function to display itself (tying mass to size).
public class Attractor
{
// The properties of an attractor
private float mass;
private float G;
private Vector3 location;
private Rigidbody body;
private GameObject attractor;
public Attractor()
{
// Create the primitive object
attractor = GameObject.CreatePrimitive(PrimitiveType.Sphere);
attractor.GetComponent<SphereCollider>().enabled = false;
// Add a rigidbody to the primitive and set body to reference the component
attractor.AddComponent<Rigidbody>();
body = attractor.GetComponent<Rigidbody>();
body.useGravity = false;
// Add a material to the object
Renderer renderer = attractor.GetComponent<Renderer>();
renderer.material = new Material(Shader.Find("Diffuse"));
renderer.material.color = Color.red;
// Set mass and G
body.mass = 20f;
G = 9.8f;
}
public Vector3 Attract(Rigidbody m)
{
Vector3 force = body.position - m.position;
float distance = force.magnitude;
// Remember we need to constrain the distance so that our circle doesn't spin out of control
distance = Mathf.Clamp(distance, 5f, 25f);
force.Normalize();
float strength = G * (body.mass * m.mass) / (distance * distance);
force *= strength;
return force;
}
public void CalculatePosition()
{
attractor.transform.position = location;
}
}
And in our main program, we can add an instance of the Attractor class.
public class Chapter2Fig6 : MonoBehaviour
{
// A Mover and an Attractor
Mover2_6 m;
Attractor a;
// Start is called before the first frame update
void Start()
{
m = new Mover2_6();
a = new Attractor();
}
// Update is called once per frame
void FixedUpdate()
{
// Apply the attraction from the Attractor on the Mover
Vector2 force = a.Attract(m.body);
m.ApplyForce(force);
m.CalculatePosition();
a.CalculatePosition();
}
}
This is a good structure: a main program with a Mover and an Attractor object, and a class to handle the variables and behaviors of movers and attractors. The last piece of the puzzle is how to get one object to attract the other. How do we get these two objects to talk to each other?
There are a number of ways we could do this. Here are just a few possibilities.
| Task | Function |
|---|---|
| 1. A function that receives both an Attractor and a Mover: | attraction(a,m); |
| 2. A function in the Attractor class that receives a Mover: | a.attract(m); |
| 3. A function in the Mover class that receives an Attractor: | m.attractedTo(a); |
| A function in the Attractor class that receives a Mover and returns a Vector2, which is the attraction force. That attraction force is then passed into the Mover's AddForce() function | Vector2 f = a.attract(m); m.AddForce(f); |
and so on. . .
It’s good to look at a range of options for making objects talk to each other, and you could probably make arguments for each of the above possibilities. I’d like to at least discard the first one, since an object-oriented approach is really a much better choice over an arbitrary function not tied to either the Mover or Attractor class. Whether you pick option 2 or option 3 is the difference between saying “The attractor attracts the mover” or “The mover is attracted to the attractor.” Number 4 is really my favorite, at least in terms of where we are in this book. After all, we spent a lot of time working out the AddForce() function, and I think our examples will be clearer if we continue with the same methodology.
In other words, where we once had:
Vector2 force = new Vector2 (0, 0.1f, 0);
m.ApplyForce(force);
We now have:
Vector2 force = a.Attract(m.body);
m.ApplyForce(force);
And so our Update() function can now be written as:
void FixedUpdate()
{
// Apply the attraction from the Attractor on the Mover
Vector2 force = a.Attract(m.body);
m.ApplyForce(force);
m.CalculatePosition();
a.CalculatePosition();
}
We’re almost there. Since we decided to put the attract() function inside of the Attractor class, we’ll need to actually write that function. The function needs to receive a Mover object and return a Vector2, i.e.:
And what goes inside that function? All of that nice math we worked out for gravitational attraction!
public Vector3 Attract(Rigidbody m)
{
Vector3 force = body.position - m.position;
float distance = force.magnitude;
force.Normalize();
float strength = G * (body.mass * m.mass) / (distance * distance);
force *= strength;
return force;
}
And we’re done. Sort of. Almost. There’s one small kink we need to work out. Let’s look at the above code again. See that symbol for divide, the slash? Whenever we have one of these, we need to ask ourselves the question: What would happen if the distance happened to be a really, really small number or (even worse!) zero??! Well, we know we can’t divide a number by 0, and if we were to divide a number by something like 0.0001, that is the equivalent of multiplying that number by 10,000! Yes, this is the real-world formula for the strength of gravity, but we don’t live in the real world. We live in the Unity Remix world. And in the Remix world, the mover could end up being very, very close to the attractor and the force could become so strong the mover would just fly way off the screen. And so with this formula, it’s good for us to be practical and constrain the range of what distance can actually be. Maybe, no matter where the Mover actually is, we should never consider it less than 5 pixels or more than 25 pixels away from the attractor.
distance = Mathf.Clamp(distance, 5f, 25f);
For the same reason that we need to constrain the minimum distance, it’s useful for us to do the same with the maximum. After all, if the mover were to be, say, 500 pixels from the attractor (not unreasonable), we’d be dividing the force by 250,000. That force might end up being so weak that it’s almost as if we’re not applying it at all.
Now, it’s really up to you to decide what behaviors you want. But in the case of, “I want reasonable-looking attraction that is never absurdly weak or strong,” then constraining the distance is a good technique.
Our Mover class hasn’t changed at all, so let’s just look at the main program and the Attractor class as a whole, adding a variable G for the universal gravitational constant. (On the website, you’ll find that this example also has code that allows you to move the Attractor object with the mouse.)
Example 2.6: Attraction
And we could, of course, expand this example using a list to include many Mover objects, just as we did with friction and drag:
Example 2.7: Attraction with many Movers
Exercise 2.8
In the example above, we have a system (i.e. array) of Mover objects and one Attractor object. Build an example that has systems of both movers and attractors. What if you make the attractors invisible? Can you create a pattern/design from the trails of objects moving around attractors? See the Metropop Denim project by Clayton Cubitt and Tom Carden for an example.
Exercise 2.9
It’s worth noting that gravitational attraction is a model we can follow to develop our own forces. This chapter isn’t suggesting that you should exclusively create scenes that use gravitational attraction. Rather, you should be thinking creatively about how to design your own rules to drive the behavior of objects. For example, what happens if you design a force that is weaker the closer it gets and stronger the farther it gets? Or what if you design your attractor to attract faraway objects, but repel close ones?
2.10 Everything Attracts (or Repels) Everything
Hopefully, you found it helpful that we started with a simple scenario—one object attracts another object—and moved on to one object attracts many objects. However, it’s likely that you are going to find yourself in a slightly more complex situation: many objects attract each other. In other words, every object in a given system attracts every other object in that system (except for itself).
We’ve really done almost all of the work for this already. Let’s consider a Unity scene with an array of Mover objects:
The FixedUpdate() function is where we need to work some magic. Currently, we’re saying: “for every mover i, update and display yourself.” Now what we need to say is: “for every mover i, be attracted to every other mover j, and update and display yourself.” To do this, we need to nest a second loop.
void FixedUpdate()
{
// We want to create two groups of movers to iterate through.
// We do this so that a mover never tries to attract itself
for (int i = 0; i < movers.Count; i++)
{
for (int j = 0; j < movers.Count; j++)
{
if (i != j)
{
//Now that we are sure that our Mover will not attract itself, we need it to attract a different Mover
//We do that by directing a mover to use their Attract() method on another mover Rigidbody
Vector2 attractedMover = movers[j].Attract(movers[i].body);
//We then apply that force the mover with the Rigidbody's Addforce() method
movers[i].body.AddForce(attractedMover, ForceMode.Impulse);
}
}
//Now we check the boundaries of our scene to make sure the movers don't fly off
//When we use gravity, the Movers will naturally fall out of the camera's view
// This stops that.
movers[i].CheckEdges();
}
}
In the previous example, we had an Attractor object with a function named Attract(). Now, since we have movers attracting movers, all we need to do is copy the Attract() function into the Mover class.
public Vector2 Attract(Rigidbody m)
{
Vector2 force = body.position - m.position;
float distance = force.magnitude;
// Remember we need to constrain the distance so that our circle doesn't spin out of control
distance = Mathf.Clamp(distance, 5f, 25f);
force.Normalize();
float strength = (9.81f * body.mass * m.mass) / (distance * distance);
force *= strength;
return force;
}
Of course, there’s one small problem. When we are looking at every mover i and every mover j, are we OK with the times that i equals j? For example, should mover #3 attract mover #3? The answer, of course, is no. If there are five objects, we only want mover #3 to attract 0, 1, 2, and 4, skipping itself. And so, we finish this example by adding a simple conditional statement to skip applying the force when i equals j.
if (i != j)
{
//Now that we are sure that our Mover will not attract itself, we need it to attract a different Mover
//We do that by directing a mover to use their Attract() method on another mover Rigidbody
Vector2 attractedMover = movers[j].Attract(movers[i].body);
//We then apply that force the mover with the Rigidbody's Addforce() method
movers[i].body.AddForce(attractedMover, ForceMode.Impulse);
}
Example 2.8: Mutual Attraction
Exercise 2.10
Change the attraction force in Example 2.8 to a repulsion force. Can you create an example in which all of the Mover objects are attracted to the mouse, but repel each other? Think about how you need to balance the relative strength of the forces and how to most effectively use distance in your force calculations.
The Ecosystem Project
Step 2 Exercise:
Incorporate the concept of forces into your ecosystem. Try introducing other elements into the environment (food, a predator) for the creature to interact with. Does the creature experience attraction or repulsion to things in its world? Can you think more abstractly and design forces based on the creature’s desires or goals?

