Chapter 6. Autonomous Agents
“This is an exercise in fictional science, or science fiction, if you like that better.”— Valentino Braitenberg
Believe it or not, there is a purpose. Well, at least there’s a purpose to the first five chapters of this book. We could stop right here; after all, we’ve looked at several different ways of modeling motion and simulating physics. Angry Birds, here we come!
Still, let’s think for a moment. Why are we here? The nature of code, right? What have we been designing so far? Inanimate objects. Lifeless shapes sitting on our screens that flop around when affected by forces in their environment. What if we could breathe life into those shapes? What if those shapes could live by their own rules? Can shapes have hopes and dreams and fears? This is what we are here in this chapter to do—develop autonomous agents.
6.1 Forces from Within
The term autonomous agent generally refers to an entity that makes its own choices about how to act in its environment without any influence from a leader or global plan. For us, “acting” will mean moving. This addition is a significant conceptual leap. Instead of a box sitting on a boundary waiting to be pushed by another falling box, we are now going to design a box that has the ability and “desire” to leap out of the way of that other falling box, if it so chooses. While the concept of forces that come from within is a major shift in our design thinking, our code base will barely change, as these desires and actions are simply that—forces.
Here are three key components of autonomous agents that we’ll want to keep in mind as we build our examples.
An autonomous agent has a limited ability to perceive environment. It makes sense that a living, breathing being should have an awareness of its environment. What does this mean for us, however? As we look at examples in this chapter, we will point out programming techniques for allowing objects to store references to other objects and therefore “perceive” their environment. It’s also crucial that we consider the word limited here. Are we designing an all-knowing rectangle that flies around a Unity window, aware of everything else in that window? Or are we creating a shape that can only examine any other object within fifteen pixels of itself? Of course, there is no right answer to this question; it all depends. We’ll explore some possibilities as we move forward. For a simulation to feel more “natural,” however, limitations are a good thing. An insect, for example, may only be aware of the sights and smells that immediately surround it. For a real-world creature, we could study the exact science of these limitations. Luckily for us, we can just make stuff up and try it out.
An autonomous agent processes the information from its environment and calculates an action. This will be the easy part for us, as the action is a force. The environment might tell the agent that there’s a big scary-looking shark swimming right at it, and the action will be a powerful force in the opposite direction.
An autonomous agent has no leader. This third principle is something we care a little less about. After all, if you are designing a system where it makes sense to have a leader barking commands at various entities, then that’s what you’ll want to implement. Nevertheless, many of these examples will have no leader for an important reason. As we get to the end of this chapter and examine group behaviors, we will look at designing collections of autonomous agents that exhibit the properties of complex systems— intelligent and structured group dynamics that emerge not from a leader, but from the local interactions of the elements themselves.
In the late 1980s, computer scientist Craig Reynolds developed algorithmic steering behaviors for animated characters. These behaviors allowed individual elements to navigate their digital environments in a “lifelike” manner with strategies for fleeing, wandering, arriving, pursuing, evading, etc. Used in the case of a single autonomous agent, these behaviors are fairly simple to understand and implement. In addition, by building a system of multiple characters that steer themselves according to simple, locally based rules, surprising levels of complexity emerge. The most famous example is Reynolds’s “boids” model for “flocking/swarming” behavior.
6.2 Vehicles and Steering
Now that we understand the core concepts behind autonomous agents, we can begin writing the code. There are many places where we could start. Artificial simulations of ant and termite colonies are fantastic demonstrations of systems of autonomous agents. (For more on this topic, I encourage you to read Turtles, Termites, and Traffic Jams by Mitchel Resnick.) However, we want to begin by examining agent behaviors that build on the work we’ve done in the first five chapters of this book: modeling motion with vectors and driving motion with forces. This time we are going to call it Vehicle.
public class VehicleChapter6_1 : MonoBehaviour
{
public float r;
public float mass;
private GameObject vehicle;
public GameObject target;
private Rigidbody body;
}
In his 1999 paper “Steering Behaviors for Autonomous Characters,” Reynolds uses the word “vehicle” to describe his autonomous agents, so we will follow suit.
Why Vehicle?
In 1986, Italian neuroscientist and cyberneticist Valentino Braitenberg described a series of hypothetical vehicles with simple internal structures in his book Vehicles: Experiments in Synthetic Psychology. Braitenberg argues that his extraordinarily simple mechanical vehicles manifest behaviors such as fear, aggression, love, foresight, and optimism. Reynolds took his inspiration from Braitenberg, and we’ll take ours from Reynolds.
Reynolds describes the motion of idealized vehicles (idealized because we are not concerned with the actual engineering of such vehicles, but simply assume that they exist and will respond to our rules) as a series of three layers—Action Selection, Steering, and Locomotion.
Action Selection. A vehicle has a goal (or goals) and can select an action (or a combination of actions) based on that goal. This is essentially where we left off with autonomous agents. The vehicle takes a look at its environment and calculates an action based on a desire: “I see a zombie marching towards me. Since I don’t want my brains to be eaten, I’m going to flee from the zombie.” The goal is to keep one’s brains and the action is to flee. Reynolds’s paper describes many goals and associated actions such as: seek a target, avoid an obstacle, and follow a path. In a moment, we’ll start building these examples out with Unity code.
Steering. Once an action has been selected, the vehicle has to calculate its next move. For us, the next move will be a force; more specifically, a steering force. Luckily, Reynolds has developed a simple steering force formula that we’ll use throughout the examples in this chapter: steering force = desired velocity - current velocity. We’ll get into the details of this formula and why it works so effectively in the next section.
Locomotion. For the most part, we’re going to ignore this third layer. In the case of fleeing zombies, the locomotion could be described as “left foot, right foot, left foot, right foot, as fast as you can.” In our Unity world, however, a rectangle or circle or triangle’s actual movement across a window is irrelevant given that it’s all an illusion in the first place. Nevertheless, this isn’t to say that you should ignore locomotion entirely. You will find great value in thinking about the locomotive design of your vehicle and how you choose to animate it. The examples in this chapter will remain visually bare, and a good exercise would be to elaborate on the animation style —could you add spinning wheels or oscillating paddles or shuffling legs?
Ultimately, the most important layer for you to consider is #1—Action Selection. What are the elements of your system and what are their goals? In this chapter, we are going to look at a series of steering behaviors (i.e. actions): seek, flee, follow a path, follow a flow field, flock with your neighbors, etc. It’s important to realize, however, that the point of understanding how to write the code for these behaviors is not because you should use them in all of your projects. Rather, these are a set of building blocks, a foundation from which you can design and develop vehicles with creative goals and new and exciting behaviors. And even though we will think literally in this chapter (follow that pixel!), you should allow yourself to think more abstractly (like Braitenberg). What would it mean for your vehicle to have “love” or “fear” as its goal, its driving force? Finally (and we’ll address this later in the chapter), you won’t get very far by developing simulations with only one action. Yes, our first example will be “seek a target.” But for you to be creative—to make these steering behaviors your own—it will all come down to mixing and matching multiple actions within the same vehicle. So view these examples not as singular behaviors to be emulated, but as pieces of a larger puzzle that you will eventually assemble.
6.3 The Steering Force
We can entertain ourselves by discussing the theoretical principles behind autonomous agents and steering as much as we like, but we can’t get anywhere without first understanding the concept of a steering force. Consider the following scenario. A vehicle moving with velocity desires to seek a target.
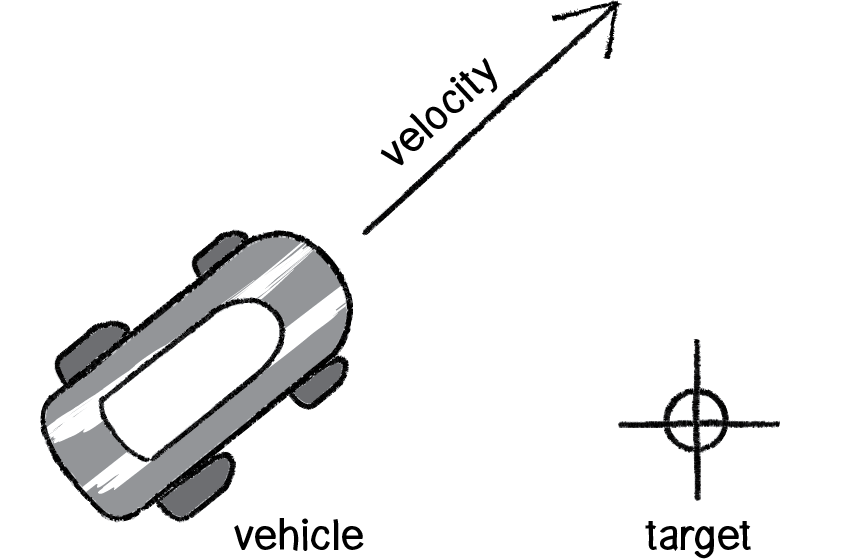
Figure 6.1
Its goal and subsequent action is to seek the target in Figure 6.1. If you think back to Chapter 2, you might begin by making the target an attractor and apply a gravitational force that pulls the vehicle to the target. This would be a perfectly reasonable solution, but conceptually it’s not what we’re looking for here. We don’t want to simply calculate a force that pushes the vehicle towards its target; rather, we are asking the vehicle to make an intelligent decision to steer towards the target based on its perception of its state and environment (i.e. how fast and in what direction is it currently moving). The vehicle should look at how it desires to move (a vector pointing to the target), compare that goal with how quickly it is currently moving (its velocity), and apply a force accordingly.
steering force = desired velocity - current velocity
Or as we might write in Unity:
Vector3 steer = desired - body.velocity;
In the above formula, velocity is no problem. After all, we’ve got a variable for that. However, we don’t have the desired velocity; this is something we have to calculate. Let’s take a look at Figure 6.2. If we’ve defined the vehicle’s goal as “seeking the target,” then its desired velocity is a vector that points from its current location to the target location.
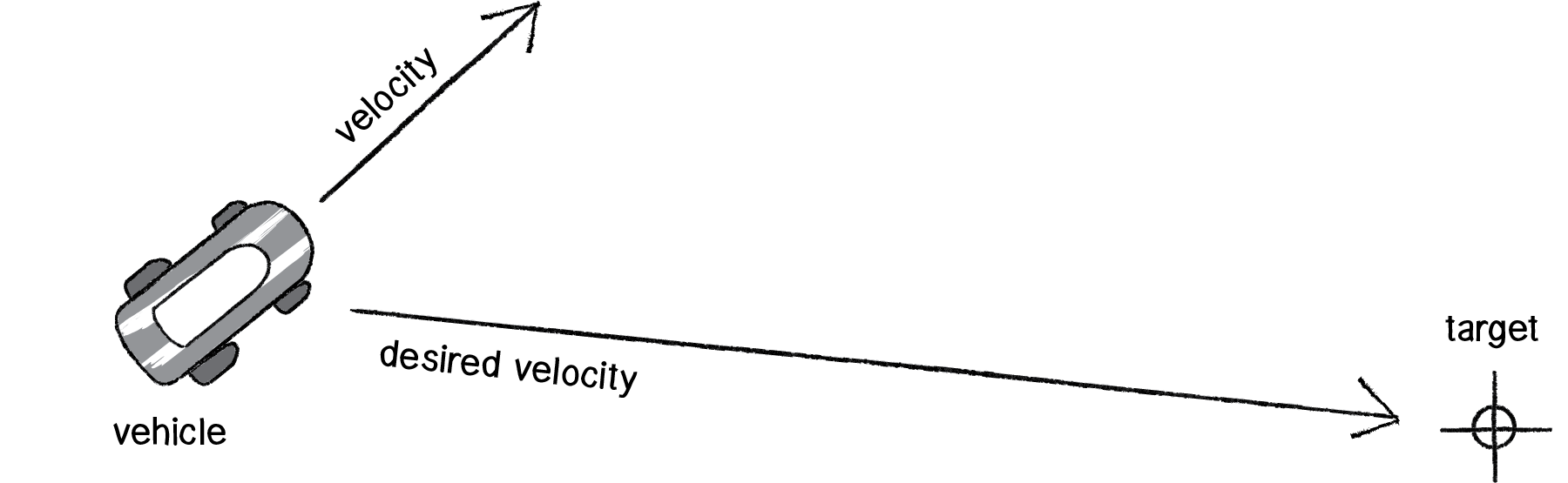
Figure 6.1
Assuming a Vector3 target, we then have:
Vector3 desired = target - body.transform.position;
But this isn’t particularly realistic. What if we have a very high-resolution window and the target is thousands of pixels away? Sure, the vehicle might desire to teleport itself instantly to the target location with a massive velocity, but this won’t make for an effective animation. What we really want to say is:
The vehicle desires to move towards the target at maximum speed.
In other words, the vector should point from location to target and with a magnitude equal to maximum speed (i.e. the fastest the vehicle can go). So first, we need to make sure we add a variable to our Vehicle class that stores maximum speed.
public class VehicleChapter6_1
{
public float r;
public float maxspeed;
public float mass;
private GameObject vehicle;
public GameObject target;
private Rigidbody body;
}
Then, in our desired velocity calculation, we scale according to maximum speed.
Vector3 desired = target - body.transform.position;
desired.Normalize();
desired *= maxspeed;
Putting this all together, we can write a function called seek() that receives a Vector3 target and calculates a steering force towards that target.
public void Seek(Vector3 target)
{
Vector3 desired = target - body.transform.position;
desired.Normalize();
desired *= maxspeed;
Vector3 steer = desired - body.velocity;
ApplyForce(steer);
}
Note how in the above function we finish by passing the steering force into applyForce(). This assumes that we are basing this example on the foundation we built in Chapter 2. However, you could just as easily use the steering force with Box2D’s applyForce() function or toxiclibs’ addForce() function.
So why does this all work so well? Let’s see what the steering force looks like relative to the vehicle and target locations.
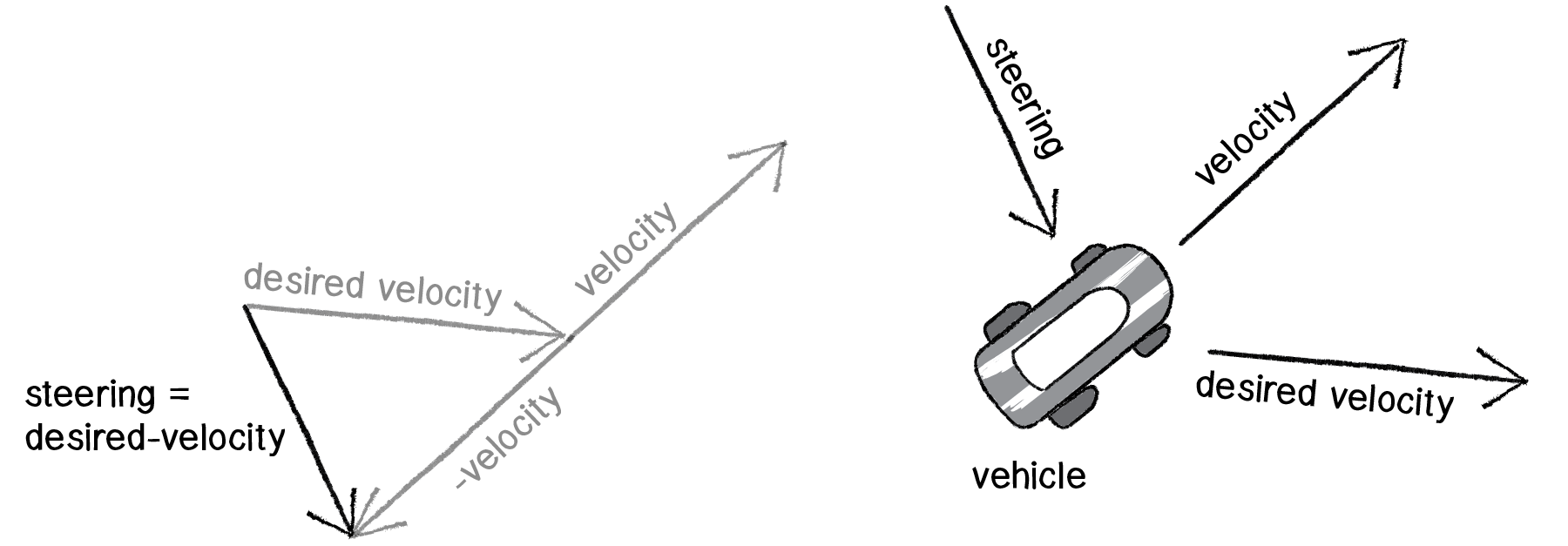
Figure 6.4
Again, notice how this is not at all the same force as gravitational attraction. Remember one of our principles of autonomous agents: An autonomous agent has a limited ability to perceive its environment. Here is that ability, subtly embedded into Reynolds’s steering formula. If the vehicle weren’t moving at all (zero velocity), desired minus velocity would be equal to desired. But this is not the case. The vehicle is aware of its own velocity and its steering force compensates accordingly. This creates a more active simulation, as the way in which the vehicle moves towards the targets depends on the way it is moving in the first place.
In all of this excitement, however, we’ve missed one last step. What sort of vehicle is this? Is it a super sleek race car with amazing handling? Or a giant Mack truck that needs a lot of advance notice to turn? A graceful panda, or a lumbering elephant? Our example code, as it stands, has no feature to account for this variability in steering ability. Steering ability can be controlled by limiting the magnitude of the steering force. Let’s call that limit the “maximum force” (or maxforce for short). And so finally, we have:
public class VehicleChapter6_1 : MonoBehaviour
{
public float r;
public float maxforce;
public float maxspeed;
public float mass;
}
followed by:
public void Seek(Vector3 target)
{
Vector3 desired = target - body.transform.position;
desired.Normalize();
desired *= maxspeed;
Vector3 steer = desired - body.velocity;
steer.x = Mathf.Clamp(steer.x, -maxforce, maxforce);
steer.y = Mathf.Clamp(steer.y, -maxforce, maxforce);
steer.z = Mathf.Clamp(steer.z, -maxforce, maxforce);
ApplyForce(steer);
}
Limiting the steering force brings up an important point. We must always remember that it’s not actually our goal to get the vehicle to the target as fast as possible. If that were the case, we would just say “location equals target” and there the vehicle would be. Our goal, as Reynolds puts it, is to move the vehicle in a “lifelike and improvisational manner.” We’re trying to make it appear as if the vehicle is steering its way to the target, and so it’s up to us to play with the forces and variables of the system to simulate a given behavior. For example, a large maximum steering force would result in a very different path than a small one. One is not inherently better or worse than the other; it depends on your desired effect. (And of course, these values need not be fixed and could change based on other conditions. Perhaps a vehicle has health: the higher the health, the better it can steer.)
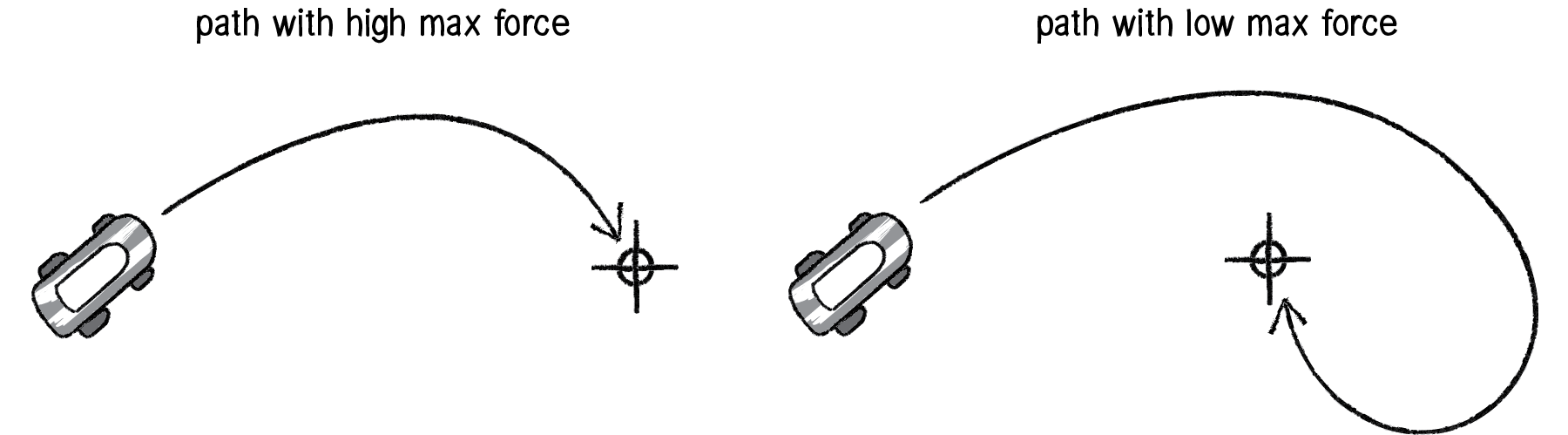
Figure 6.5
Here is the full Vehicle class, incorporating the rest of the elements from the Chapter 2 Mover object.
Example 6.1: Seeking a target
Exercise 6.1
Implement a “fleeing” steering behavior (desired vector is inverse of “seek”).
Exercise 6.2
Implement seeking a moving target, often referred to as “pursuit.” In this case, your desired vector won’t point towards the object’s current location, but rather its “future” location as extrapolated from its current velocity. We’ll see this ability for a vehicle to “predict the future” in later examples.
Hint: Look at the normal of the object's velocity and extrapolate from that number.
Exercise 6.3
Create a scene where a vehicle’s maximum force and maximum speed do not remain constant, but rather vary according to environmental factors.
6.4 Arriving Behavior
After working for a bit with the seeking behavior, you are probably asking yourself, “What if I want my vehicle to slow down as it approaches the target?” Before we can even begin to answer this question, we should look at the reasons behind why the seek behavior causes the vehicle to fly past the target so that it has to turn around and go back. Let’s consider the brain of a seeking vehicle. What is it thinking?
Frame 1: I want to go as fast as possible towards the target!
Frame 2: I want to go as fast as possible towards the target!
Frame 3: I want to go as fast as possible towards the target!
Frame 4: I want to go as fast as possible towards the target!
Frame 5: I want to go as fast as possible towards the target!
etc.
The vehicle is so gosh darn excited about getting to the target that it doesn’t bother to make any intelligent decisions about its speed relative to the target’s proximity. Whether it’s far away or very close, it always wants to go as fast as possible.

Figure 6.6
In some cases, this is the desired behavior (if a missile is flying at a target, it should always travel at maximum speed.) However, in many other cases (a car pulling into a parking spot, a bee landing on a flower), the vehicle’s thought process needs to consider its speed relative to the distance from its target. For example:
Frame 1: I’m very far away. I want to go as fast as possible towards the target!
Frame 2: I’m very far away. I want to go as fast as possible towards the target!
Frame 3: I’m somewhat far away. I want to go as fast as possible towards the target!
Frame 4: I’m getting close. I want to go more slowly towards the target!
Frame 5: I’m almost there. I want to go very slowly towards the target!
Frame 6: I’m there. I want to stop!

Figure 6.7
How can we implement this “arriving” behavior in code? Let’s return to our seek() function and find the line of code where we set the magnitude of the desired velocity.
Vector3 desired = target - body.transform.position;
desired.Normalize();
desired *= maxspeed;
In Example 6.1, the magnitude of the desired vector is always “maximum” speed.
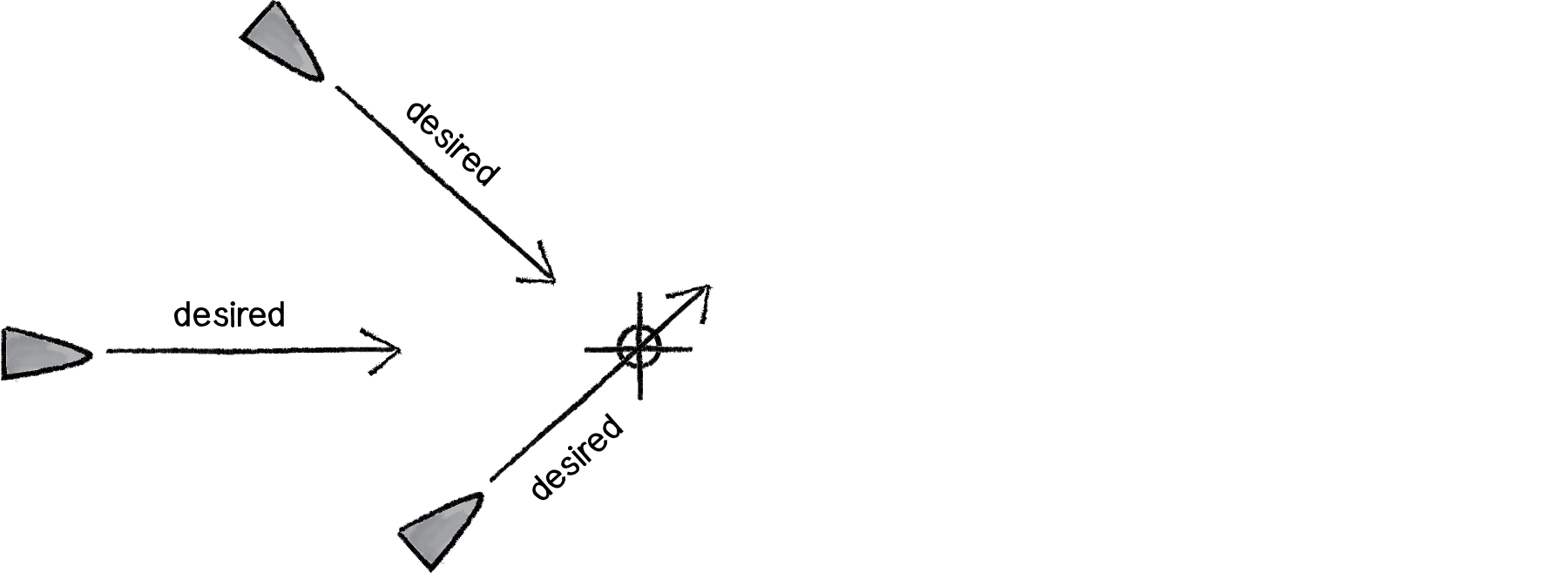
Figure 6.8
What if we instead said the desired velocity is equal to half the distance?
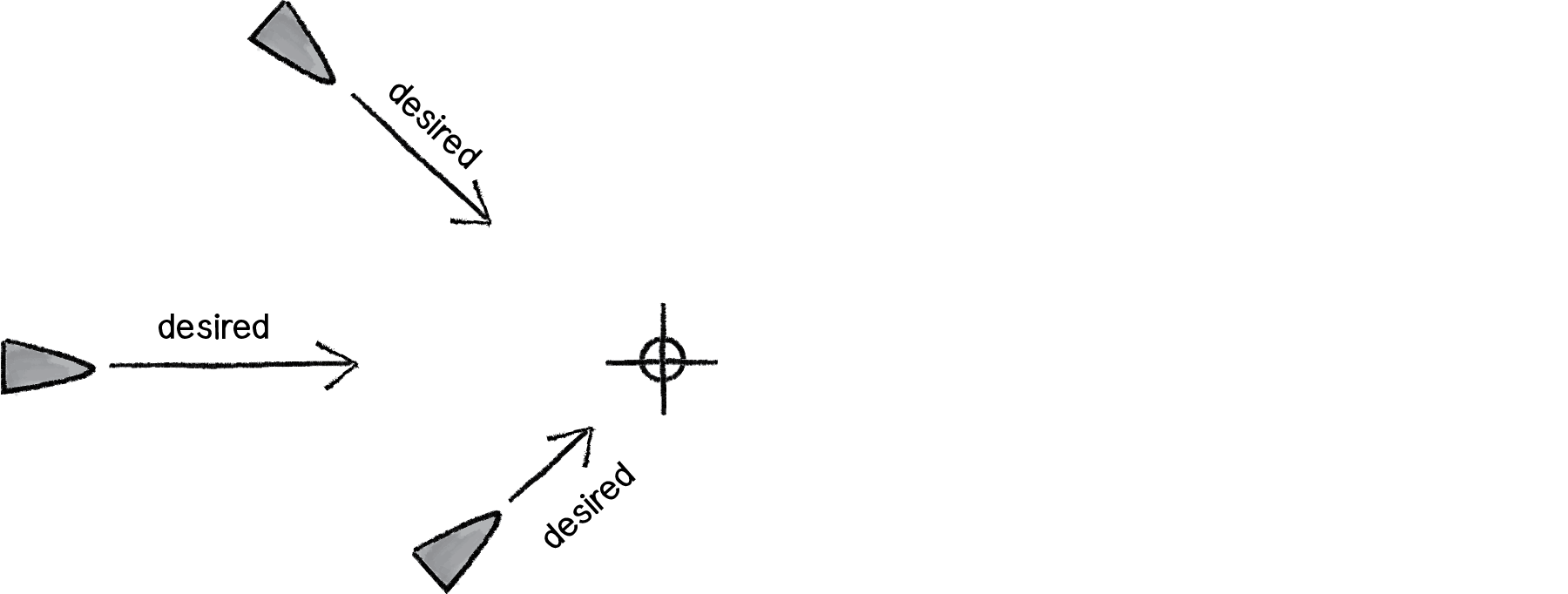
Figure 6.9
Vector3 desired = target - body.transform.position;
desired /= 2f;
While this nicely demonstrates our goal of a desired speed tied to our distance from the target, it’s not particularly reasonable. After all, 10 pixels away is rather close and a desired speed of 5 is rather large. Something like a desired velocity with a magnitude of 5% of the distance would work much better.
Vector3 desired = target - body.transform.position;
desired *= .05f;
Reynolds describes a more sophisticated approach. Let’s imagine a circle around the target with a given radius. If the vehicle is within that circle, it slows down—at the edge of the circle, its desired speed is maximum speed, and at the target itself, its desired speed is 0.
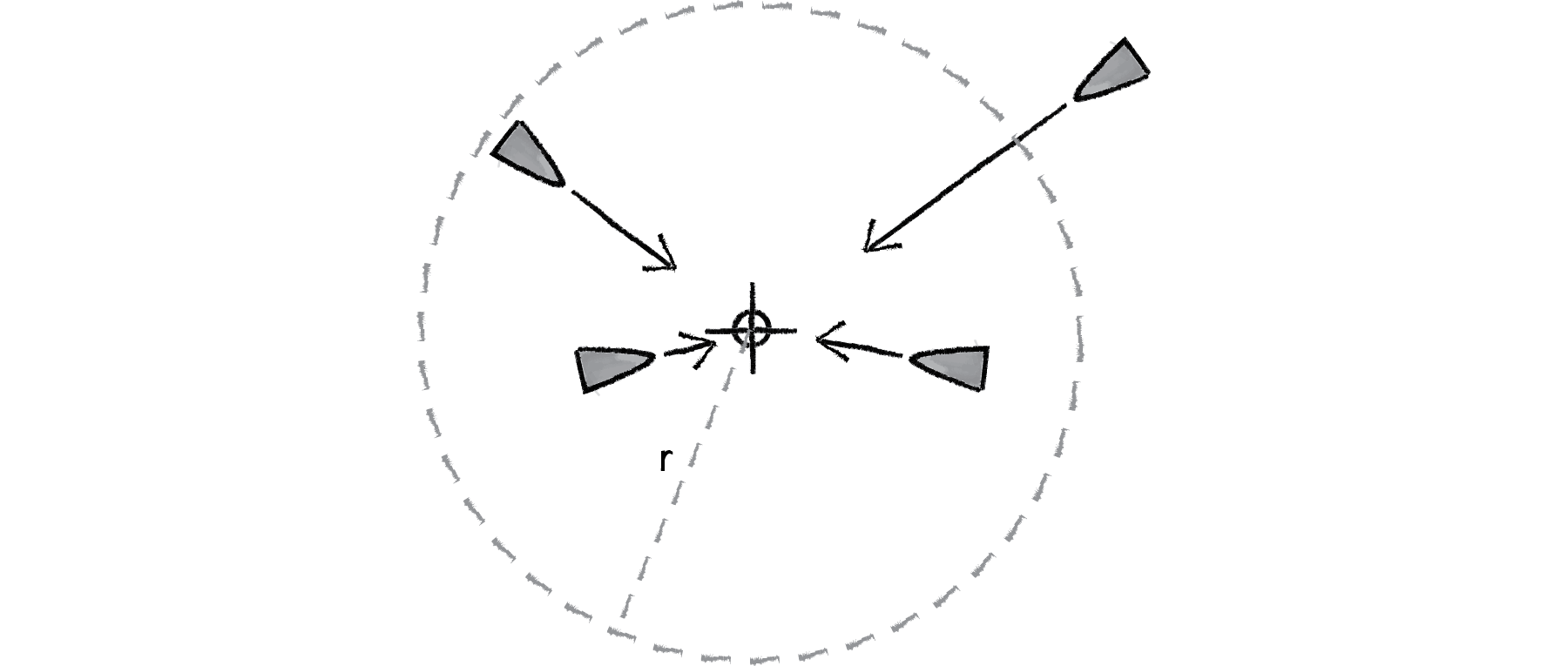
Figure 6.10
In other words, if the distance from the target is less than r, the desired speed is between 0 and maximum speed mapped according to that distance.
Example 6.2: Arrive steering behavior
The arrive behavior is a great demonstration of the magic of “desired minus velocity.” Let’s examine this model again relative to how we calculated forces in earlier chapters. In the “gravitational attraction” examples, the force always pointed directly from the object to the target (the exact direction of the desired velocity), whether the force was strong or weak.
The steering function, however, says: “I have the ability to perceive the environment.” The force isn’t based on just the desired velocity, but on the desired velocity relative to the current velocity. Only things that are alive can know their current velocity. A box falling off a table doesn’t know it’s falling. A cheetah chasing its prey, however, knows it is chasing.
The steering force, therefore, is essentially a manifestation of the current velocity’s error: "I’m supposed to be going this fast in this direction, but I’m actually going this fast in another direction. My error is the difference between where I want to go and where I am currently going." Taking that error and applying it as a steering force results in more dynamic, lifelike simulations. With gravitational attraction, you would never have a force pointing away from the target, no matter how close. But with arriving via steering, if you are moving too fast towards the target, the error would actually tell you to slow down!
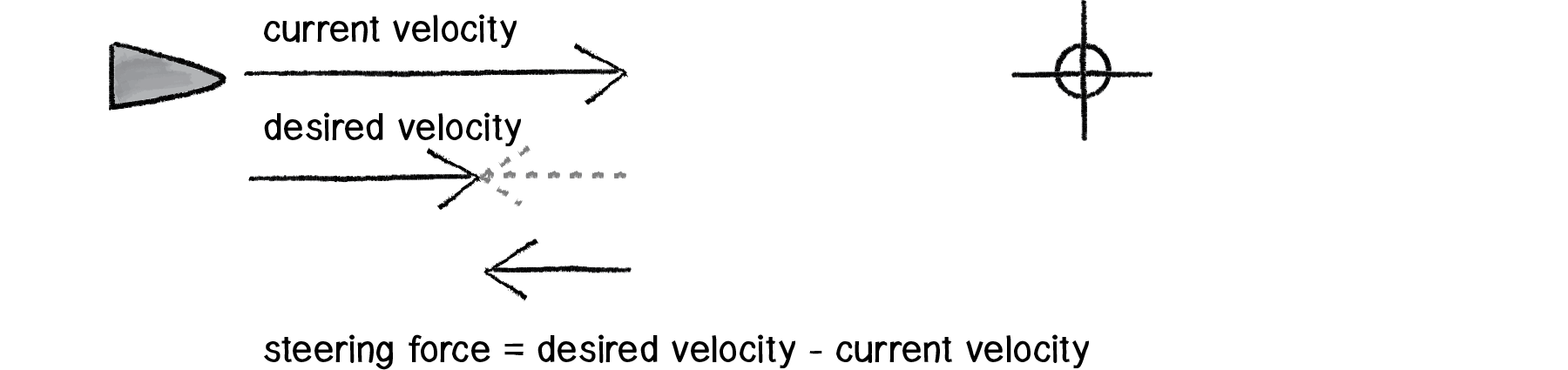
Figure 6.11
6.5 Your Own Desires: Desired Velocity
The first two examples we’ve covered—seek and arrive—boil down to calculating a single vector for each behavior: the desired velocity. And in fact, every single one of Reynolds’s steering behaviors follows this same pattern. In this chapter, we’re going to walk through several more of Reynolds’s behaviors—flow field, path-following, flocking. First, however, I want to emphasize again that these are examples—demonstrations of common steering behaviors that are useful in procedural animation. They are not the be-all and end-all of what you can do. As long as you can come up with a vector that describes a vehicle’s desired velocity, then you have created your own steering behavior.
Let’s see how Reynolds defines the desired velocity for his wandering behavior.
“Wandering is a type of random steering which has some long term order: the steering direction on one frame is related to the steering direction on the next frame. This produces more interesting motion than, for example, simply generating a random steering direction each frame.”
—Craig Reynolds
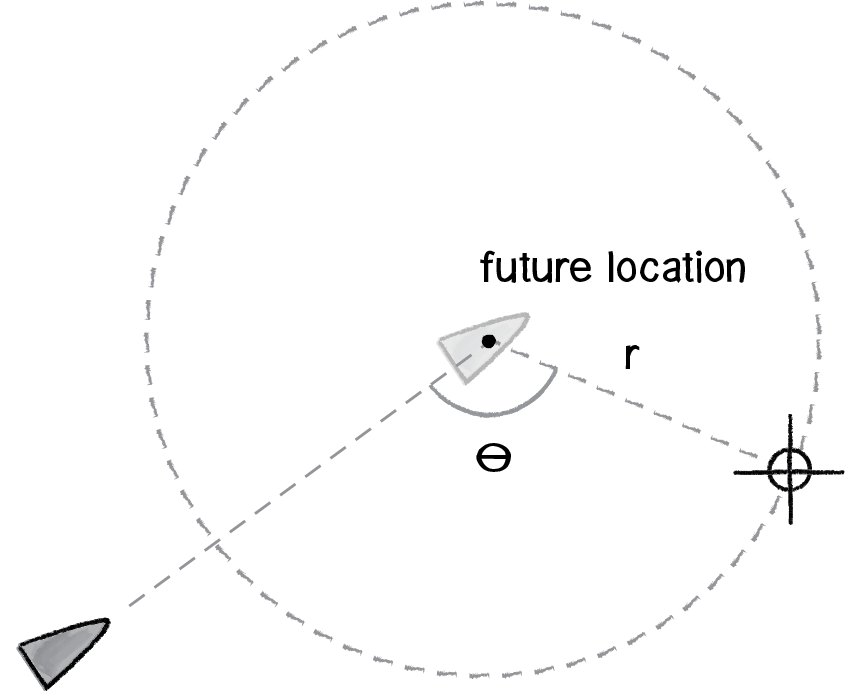
Figure 6.12
For Reynolds, the goal of wandering is not simply random motion, but rather a sense of moving in one direction for a little while, wandering off to the next for a little bit, and so on and so forth. So how does Reynolds calculate a desired vector to achieve such an effect?
Figure 6.12 illustrates how the vehicle predicts its future location as a fixed distance in front of it (in the direction of its velocity), draws a circle with radius r at that location, and picks a random point along the circumference of the circle. That random point moves randomly around the circle in each frame of animation. And that random point is the vehicle’s target, its desired vector pointing in that direction.
Sounds a bit absurd, right? Or, at the very least, rather arbitrary. In fact, this is a very clever and thoughtful solution—it uses randomness to drive a vehicle’s steering, but constrains that randomness along the path of a circle to keep the vehicle’s movement from appearing jittery, and, well, random.
But the seemingly random and arbitrary nature of this solution should drive home the point I’m trying to make—these are made-up behaviors inspired by real-life motion. You can just as easily concoct some elaborate scenario to compute a desired velocity yourself. And you should.
Exercise 6.4
Write the code for Reynolds’s wandering behavior. Use polar coordinates to calculate the vehicle’s target along a circular path.
Let’s say we want to create a steering behavior called “stay within walls.” We’ll define the desired velocity as:
If a vehicle comes within a distance d of a wall, it desires to move at maximum speed in the opposite direction of the wall.
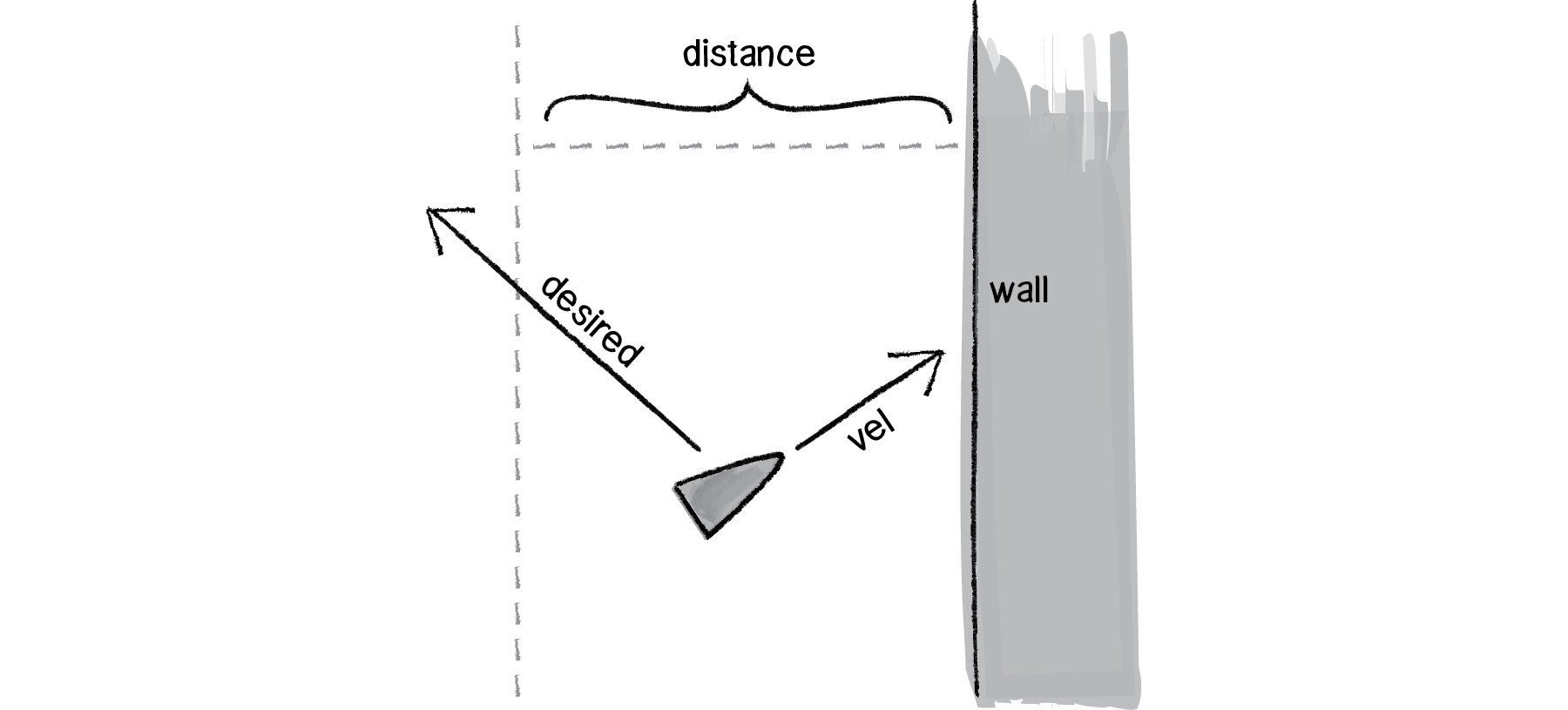
Figure 6.13
If we define the walls of the space as the edges of a Unity window and the distance d as 25, the code is rather simple.
Example 6.3: “Stay within walls” steering behavior
Exercise 6.5
Come up with your own arbitrary scheme for calculating a desired velocity.
6.6 Flow Fields
Now back to the task at hand. Let’s examine a couple more of Reynolds’s steering behaviors. First, flow field following. What is a flow field? Think of your Unity window as a grid. In each cell of the grid lives an arrow pointing in some direction—you know, a vector. As a vehicle moves around the screen, it asks, “Hey, what arrow is beneath me? That’s my desired velocity!”
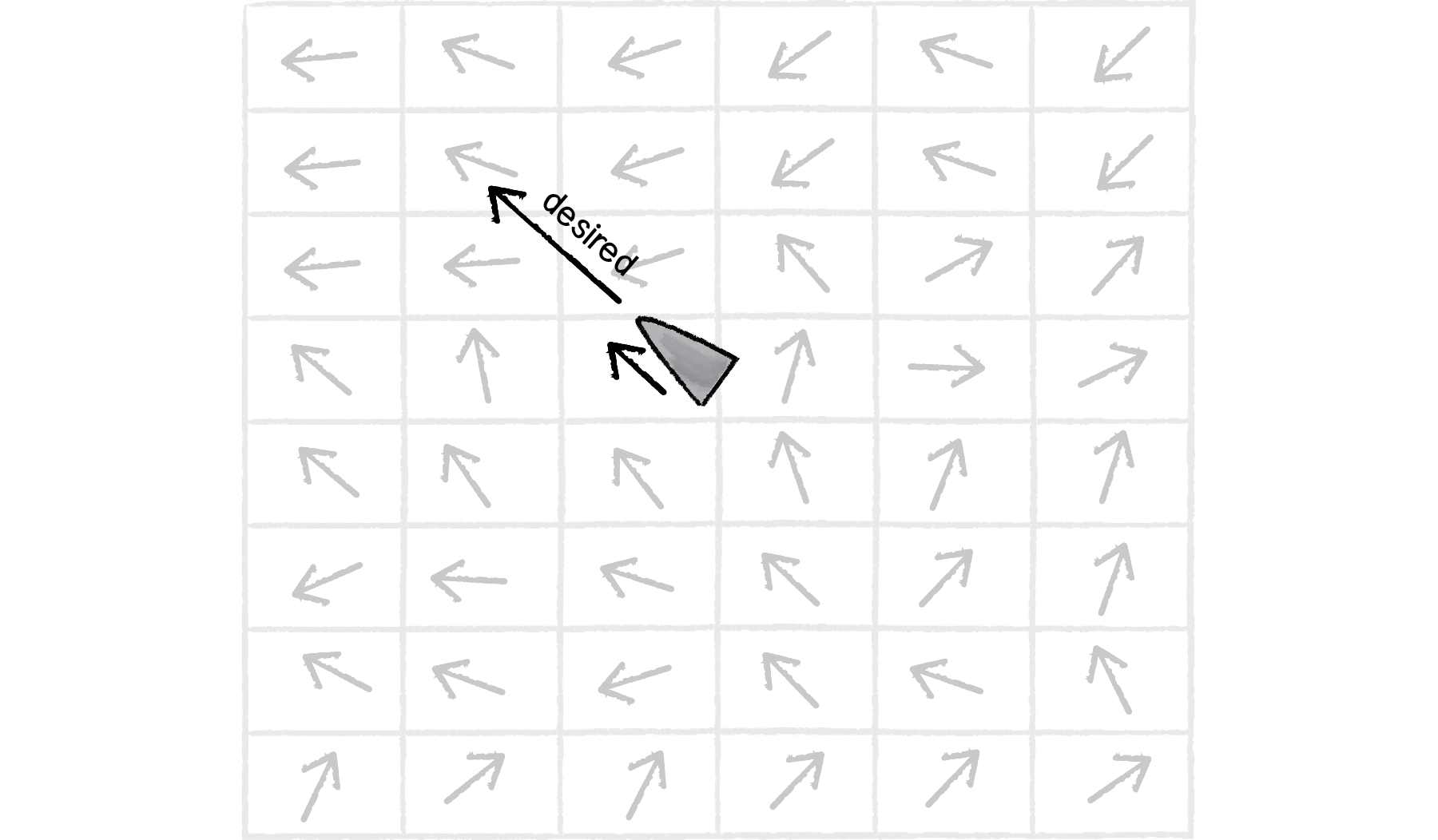
Figure 6.14
Reynolds’s flow field following example has the vehicle predicting its future location and following the vector at that spot, but for simplicity’s sake, we’ll have the vehicle simply look to the vector at its current location.
Before we can write the additional code for our Vehicle class, we’ll need to build a class that describes the flow field itself, the grid of vectors. A two-dimensional array is a convenient data structure in which to store a grid of information. If you are not familiar with 2D arrays, I suggest reviewing this online Unity tutorial: 2D array. The 2D array is convenient because we reference each element with two indices, which we can think of as columns and rows.
public class Ch6Fig4FlowField
{
// Declaring a 2D array of Vector2's
private Vector2[,] field;
// How many columns and how many rows in the grid?
private int columns, rows;
// Resolution of grid relative to window width and height in pixels
private int resolution;
// Maximum bounds of the screen
private Vector3 maximumPos;
}
Notice how we are defining a third variable called resolution above. What is this variable? Let’s say we have a Unity window that is 200 pixels wide by 200 pixels high. We could make a flow field that has a Vector3 object for every single pixel, or 40,000 Vector3s (200 * 200). This isn’t terribly unreasonable, but in our case, it’s overkill. We don’t need a Vector3 for every single pixel; we can achieve the same effect by having, say, one every ten pixels (20 * 20 = 400). We use this resolution to define the number of columns and rows based on the size of the window divided by resolution:
public Ch6Fig4FlowField()
{
FindWindowLimits();
resolution = 10;
columns = Screen.width / resolution; // Total columns equals width divided by resolution
rows = Screen.height / resolution; // Total rows equals height divided by resolution
field = new Vector2[columns, rows];
InitializeFlowField();
}
Now that we’ve set up the flow field’s data structures, it’s time to compute the vectors in the flow field itself. How do we do that? However we feel like it! Perhaps we want to have every vector in the flow field pointing to the right.
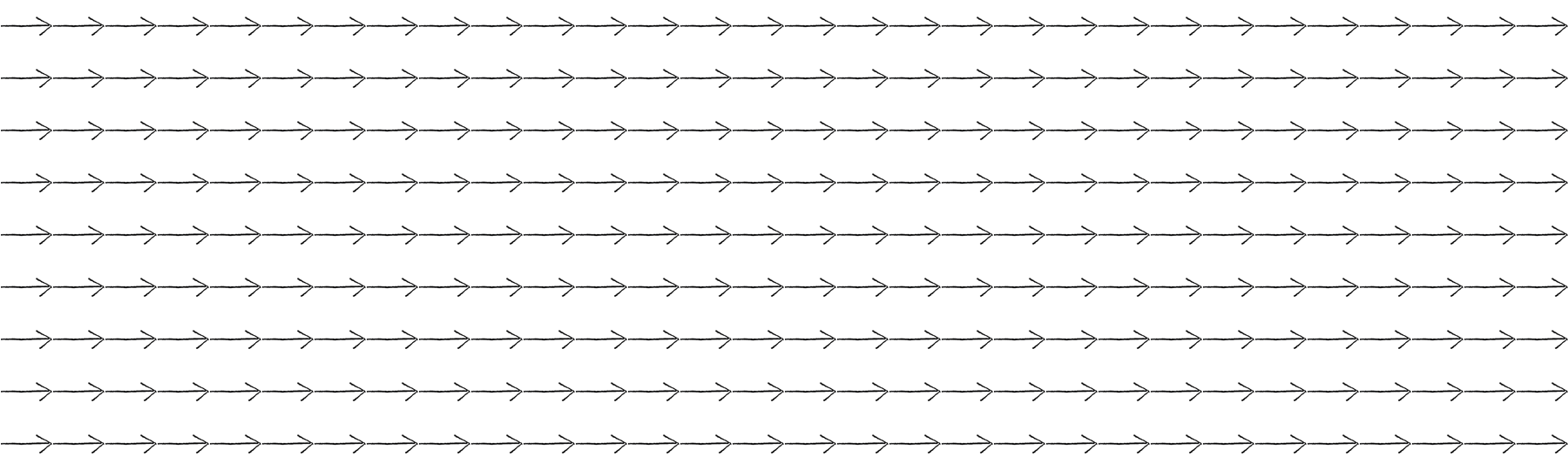
Figure 6.15
// Using a nested loop to hit every column and every row of the flow field
private void InitializeFlowField()
{
for (int i = 0; i < columns; i++)
{
for (int j = 0; j < rows; j++)
{
field[i,j] = new Vector2(1,0);
}
}
}
Or perhaps we want the vectors to point in random directions.

Figure 6.16
// Using a nested loop to hit every column and every row of the flow field
private void InitializeFlowField()
{
for (int i = 0; i < columns; i++)
{
for (int j = 0; j < rows; j++)
{
field[i,j] = Random.insideUnitCircle.normalized;
}
}
}
What if we use 2D Perlin noise (mapped to an angle)?

Figure 6.17
// Using a nested loop to hit every column and every row of the flow field
private void InitializeFlowField(GameObject flowArrow)
{
float xOff = 0;
for (int i = 0; i < columns; i++)
{
float yOff = 0;
for (int j = 0; j < rows; j++)
{
// In this example, we use Perlin noise to seed the vectors.
float noiseValue = Mathf.PerlinNoise(xOff, yOff);
// A C# recreation of Processing's Map function, which re-maps
// A number from one range to another.
// https://processing.org/reference/map_.html
float theta = 0 + ((Mathf.PI * 2) - 0) * ((noiseValue - 0) / (1 - 0));
Vector2 v = new Vector2(Mathf.Cos(theta), Mathf.Sin(theta));
field[i,j] = v;
// Map values i and j to minimum and maximum bounds of viewport
float x = -maximumPos.x + (i - 0) * ((maximumPos.x - -maximumPos.x) / ((columns - 1) - 0));
float y = -maximumPos.y + (j - 0) * ((maximumPos.y - -maximumPos.y) / ((rows - 1) - 0));
// Instantiate flow indicator at each point in grid
GameObject flowIndicator = Object.Instantiate(flowArrow);
flowIndicator.name = $"Indicator{i}_{j}_{v}";
flowIndicator.transform.localScale = new Vector3(.3f, .3f, .3f);
flowIndicator.transform.position = new Vector2(x, y);
// Set rotation of flow indicator to match the vector at each position
flowIndicator.transform.rotation = Quaternion.LookRotation(v);
Vector3 indicatorEulerAngles = flowIndicator.transform.rotation.eulerAngles;
flowIndicator.transform.rotation = Quaternion.Euler(indicatorEulerAngles.x + 90, indicatorEulerAngles.y, indicatorEulerAngles.z);
// Add newly instantiated indicator to a list
flowIndicators.Add(flowIndicator);
yOff += 0.1f;
}
xOff += 0.1f;
}
}
Now we’re getting somewhere. Flow fields can be used for simulating various effects, such as an irregular gust of wind or the meandering path of a river. Calculating the direction of your vectors using Perlin noise is one way to achieve such an effect. Of course, there’s no “correct” way to calculate the vectors of a flow field; it’s really up to you to decide what you’re looking to simulate.
Exercise 6.6
Write the code to calculate a Vector3 at every location in the flow field that points towards the center of a window.
Now that we have a two-dimensional array storing all of the flow field vectors, we need a way for a vehicle to look up its desired vector in the flow field. Let’s say we have a vehicle that lives at a Vector3: its location. We first need to divide by the resolution of the grid. For example, if the resolution is 10 and the vehicle is at (100,50), we need to look up column 10 and row 5.
int column = (int)(_lookUp.x, 0, columns - 1);
int row = (int)(_lookUp.y, 0, rows - 1);
Because a vehicle could theoretically wander off the Unity window, it’s also useful for us to employ the Clamp() function to make sure we don’t look outside of the flow field array. Here is a function we’ll call Lookup() that goes in the FlowField class—it receives a Vector2 (presumably the location of our vehicle), maps the values to ensure the mimimum value returns 0, and returns the corresponding flow field Vector2 for that location.
public Vector2 Lookup(Vector2 _lookUp)
{
float x = 0 + (_lookUp.x - -maximumPos.x) * ((columns - 1 - 0) / (maximumPos.x - -maximumPos.x));
float y = 0 + (_lookUp.y - -maximumPos.y) * ((rows - 1 - 0) / (maximumPos.y - -maximumPos.y));
// A method to return a Vector2 based on a location
int column = (int)Mathf.Clamp(x, 0, columns - 1);
int row = (int)Mathf.Clamp(y, 0, rows - 1);
Debug.Log($"column:{column}, row:{row}");
return field[column, row];
}
Before we move on to the Vehicle class, let’s take a look at the FlowField class all together.
public class Ch6Fig4FlowField
{
// Declaring a 2D array of Vector2's
private Vector2[,] field;
public List<GameObject> flowIndicators = new List<GameObject>();
// How many columns and how many rows in the grid?
private int columns, rows;
// Resolution of grid relative to window width and height in pixels
private int resolution;
// Maximum bounds of the screen
private Vector3 maximumPos;
public Ch6Fig4FlowField(GameObject flowArrow)
{
FindWindowLimits();
resolution = 30;
columns = Screen.width / resolution; // Total columns equals width divided by resolution
rows = Screen.height / resolution; // Total rows equals height divided by resolution
field = new Vector2[columns, rows];
InitializeFlowField(flowArrow);
}
private void InitializeFlowField(GameObject flowArrow)
{
// Using a nested loop to hit every column and every row of the flow field
float xOff = 0;
for (int i = 0; i < columns; i++)
{
float yOff = 0;
for (int j = 0; j < rows; j++)
{
// In this example, we use Perlin noise to seed the vectors.
float noiseValue = Mathf.PerlinNoise(xOff, yOff);
// A C# recreation of Processing's Map function, which re-maps
// A number from one range to another.
// https://processing.org/reference/map_.html
float theta = 0 + ((Mathf.PI * 2) - 0) * ((noiseValue - 0) / (1 - 0));
Vector2 v = new Vector2(Mathf.Cos(theta), Mathf.Sin(theta));
field[i,j] = v;
// Map values i and j to minimum and maximum bounds of viewport
float x = -maximumPos.x + (i - 0) * ((maximumPos.x - -maximumPos.x) / ((columns - 1) - 0));
float y = -maximumPos.y + (j - 0) * ((maximumPos.y - -maximumPos.y) / ((rows - 1) - 0));
// Instantiate flow indicator at each point in grid
GameObject flowIndicator = Object.Instantiate(flowArrow);
flowIndicator.name = $"Indicator{i}_{j}_{v}";
flowIndicator.transform.localScale = new Vector3(.3f, .3f, .3f);
flowIndicator.transform.position = new Vector2(x, y);
// Set rotation of flow indicator to match the vector at each position
flowIndicator.transform.rotation = Quaternion.LookRotation(v);
Vector3 indicatorEulerAngles = flowIndicator.transform.rotation.eulerAngles;
flowIndicator.transform.rotation = Quaternion.Euler(indicatorEulerAngles.x + 90, indicatorEulerAngles.y, indicatorEulerAngles.z);
// Add newly instantiated indicator to a list
flowIndicators.Add(flowIndicator);
yOff += 0.1f;
}
xOff += 0.1f;
}
}
public Vector2 Lookup(Vector2 _lookUp)
{
float x = 0 + (_lookUp.x - -maximumPos.x) * ((columns - 1 - 0) / (maximumPos.x - -maximumPos.x));
float y = 0 + (_lookUp.y - -maximumPos.y) * ((rows - 1 - 0) / (maximumPos.y - -maximumPos.y));
// A method to return a Vector2 based on a location
int column = (int)Mathf.Clamp(x, 0, columns - 1);
int row = (int)Mathf.Clamp(y, 0, rows - 1);
Debug.Log($"column:{column}, row:{row}");
return field[column, row];
}
private void FindWindowLimits()
{
// We want to start by setting the camera's projection to Orthographic mode
Camera.main.orthographic = true;
// For FindWindowLimits() to function correctly, the camera must be set to coordinates 0, 0, -10
Camera.main.transform.position = new Vector3(0, 0, -10);
// Next we grab the maximum position for the screen
maximumPos = Camera.main.ScreenToWorldPoint(new Vector2(Screen.width, Screen.height));
}
public void ShowFlowField()
{
// Set indicators active if holding space, set inactive if not
if (Input.GetKey(KeyCode.Space))
{
// Loop through flowIndicators list and set active state for each item
for (int i = 0; i < flowIndicators.Count; i++)
{
flowIndicators[i].SetActive(true);
}
}
else
{
for (int i = 0; i < flowIndicators.Count; i++)
{
flowIndicators[i].SetActive(false);
}
}
}
So let’s assume we have a FlowField object called “flow”. Using the lookup() function above, our vehicle can then retrieve a desired vector from the flow field and use Reynolds’s rules (steering = desired - velocity) to calculate a steering force.
Example 6.4: Flow field following
Exercise 6.7
Adapt the flow field example so that the Vector3s change over time. (Hint: try using the third dimension of Perlin noise!)
Exercise 6.8
Can you seed a flow field from the pixels of an Image? For example, try having the Vector3s point from dark to light colors (or vice versa).
6.7 The Dot Product
In a moment, we’re going to work through the algorithm (along with accompanying mathematics) and code for another of Craig Reynolds’s steering behaviors: Path Following. Before we can do this, however, we have to spend some time learning about another piece of vector math that we skipped in Chapter 1—the dot product. We haven’t needed it yet, but it’s likely going to prove quite useful for you (beyond just this path-following example), so we’ll go over it in detail now.
Remember all the basic vector math we covered in Chapter 1? Add, subtract, multiply, and divide?
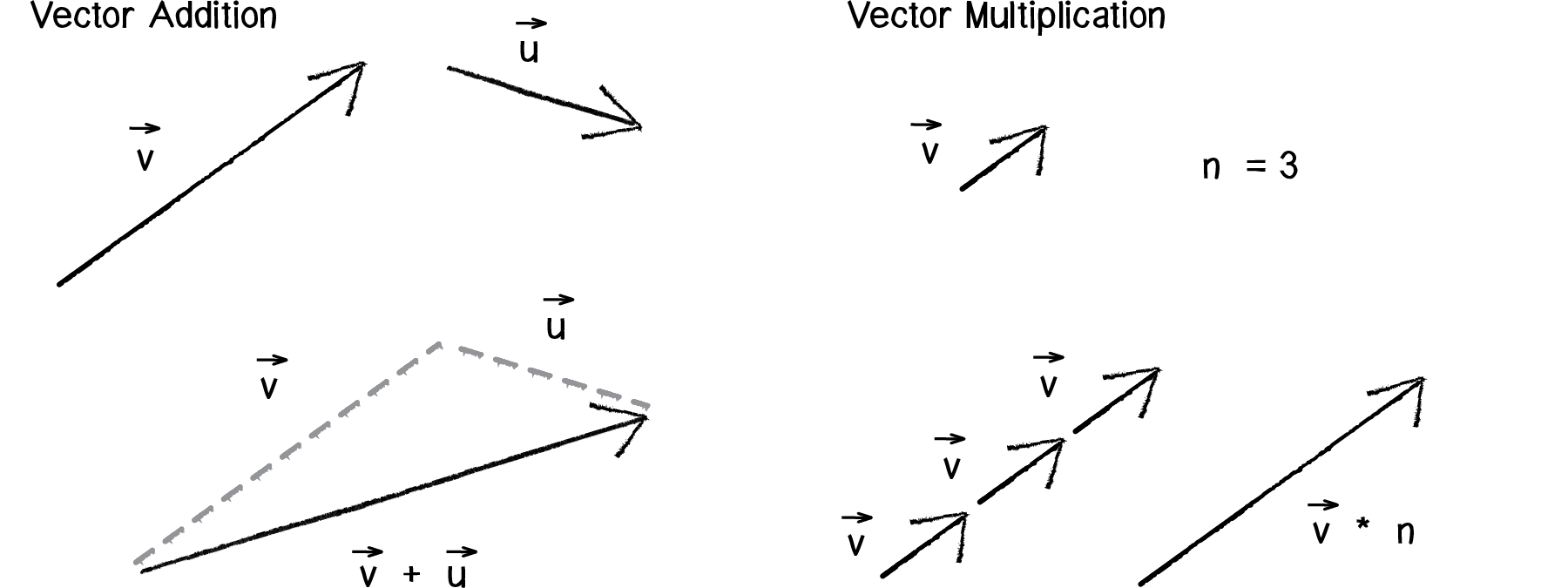
Figure 6.18
Notice how in the above diagram, vector multiplication involves multiplying a vector by a scalar value. This makes sense; when we want a vector to be twice as large (but facing the same direction), we multiply it by 2. When we want it to be half the size, we multiply it by 0.5.
However, there are two other multiplication-like operations with vectors that are useful in certain scenarios—the dot product and the cross product. For now we’re going to focus on the dot product, which is defined as follows. Assume vectors A→ and B→:
A→ = (ax,ay)
B→ = (bx,by)
THE DOT PRODUCT: A→ · B→ = ax*bx+ay*by
For example, if we have the following two vectors:
A→ = (−3,5)
B→ = (10,1)
A→ · B→ = −3*10+5*1=−30+5=35
Notice that the result of the dot product is a scalar value (a single number) and not a vector.
In Unity, this would translate to:
// Treat start as the origin of our problem.
Vector2 a = new Vector2(-3,5);
Vector2 b = new Vector2(10,1);
float n = Vector2.Dot(a, b);
The Vector3 class includes a function to calculate the dot product.
float n = a.dot(b);
This is simple enough, but why do we need the dot product, and when is it going to be useful for us in code?
One of the more common uses of the dot product is to find the angle between two vectors. Another way in which the dot product can be expressed is:
A→ · B→ = ∥A→∥ * ∥B→∥ * cos(θ)
In other words, A dot B is equal to the magnitude of A times magnitude of B times cosine of theta (with theta defined as the angle between the two vectors A and B).
The two formulas for dot product can be derived from one another with trigonometry, but for our purposes we can be happy with operating on the assumption that:
A→ · B→ = ∥A→∥ * ∥B→∥ * cos(θ)
A→ · B→ = ax*bx+ay*by
both hold true and therefore:
ax*bx+ay*by = ∥A→∥ * ∥B→∥ * cos(θ)
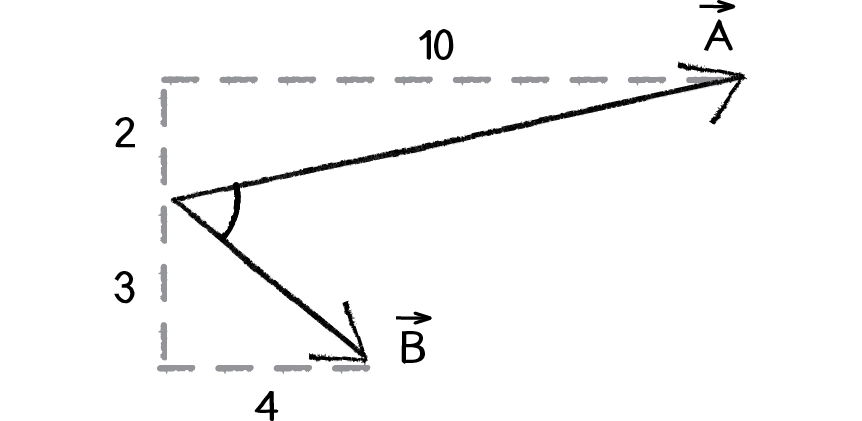
Figure 6.19
Now, let’s start with the following problem. We have the vectors A and B:
A→ = (10,2)
B→ = (4,−3)
We now have a situation in which we know everything except for theta. We know the components of the vector and can calculate the magnitude of each vector. We can therefore solve for cosine of theta:
cos(θ) = ( A→ · B→ ) / ( ∥A→∥ * ∥B→∥ )
To solve for theta, we can take the inverse cosine (often expressed as cosine-1 or arccosine).
θ = cos−1 ( ( A→ · B→ ) / ( ∥A→∥ * ∥B→∥ ) )
Let’s now do the math with actual numbers:
∥A→∥ = 10.2
∥B→∥ = 5
Therefore:
θ = cos−1 ( ( 10 * 4 + 2 * −3 ) / ( 10.2 * 5 ) )
θ = cos−1 ( 34 / 51 )
θ = ∼48∘
The Unity version of this would be:
private Vector2 GetNormalPoint(Vector2 point, Vector2 start, Vector2 end)
{
// Treat start as the origin of our problem.
Vector2 ap = point - start;
Vector2 ab = end - start;
// Scale the vector by the dot product to find the nearest point to p.
ab.Normalize();
ab *= Vector2.Dot(ap, ab);
// Re-add the relative position of our input.
Vector2 normalPoint = ab + start;
return normalPoint;
}
Exercise 6.9
Create a scene that displays the angle between two Vector3 objects.
A couple things to note here:
If two vectors (A→ and B→) are orthogonal (i.e. perpendicular), the dot product (A→ · B→) is equal to 0.
If two vectors are unit vectors, then the dot product is simply equal to cosine of the angle between them, i.e. A→ · B→ = cos(θ) if A→ and B→ are of length 1.
6.8 Path Following
Now that we’ve got a basic understanding of the dot product under our belt, we can return to a discussion of Craig Reynolds’s path-following algorithm. Let’s quickly clarify something. We are talking about path following, not path finding. Pathfinding refers to a research topic (commonly studied in artificial intelligence) that involves solving for the shortest distance between two points, often in a maze. With path following, the path already exists and we’re asking a vehicle to follow that path.
Before we work out the individual pieces, let’s take a look at the overall algorithm for path following, as defined by Reynolds.
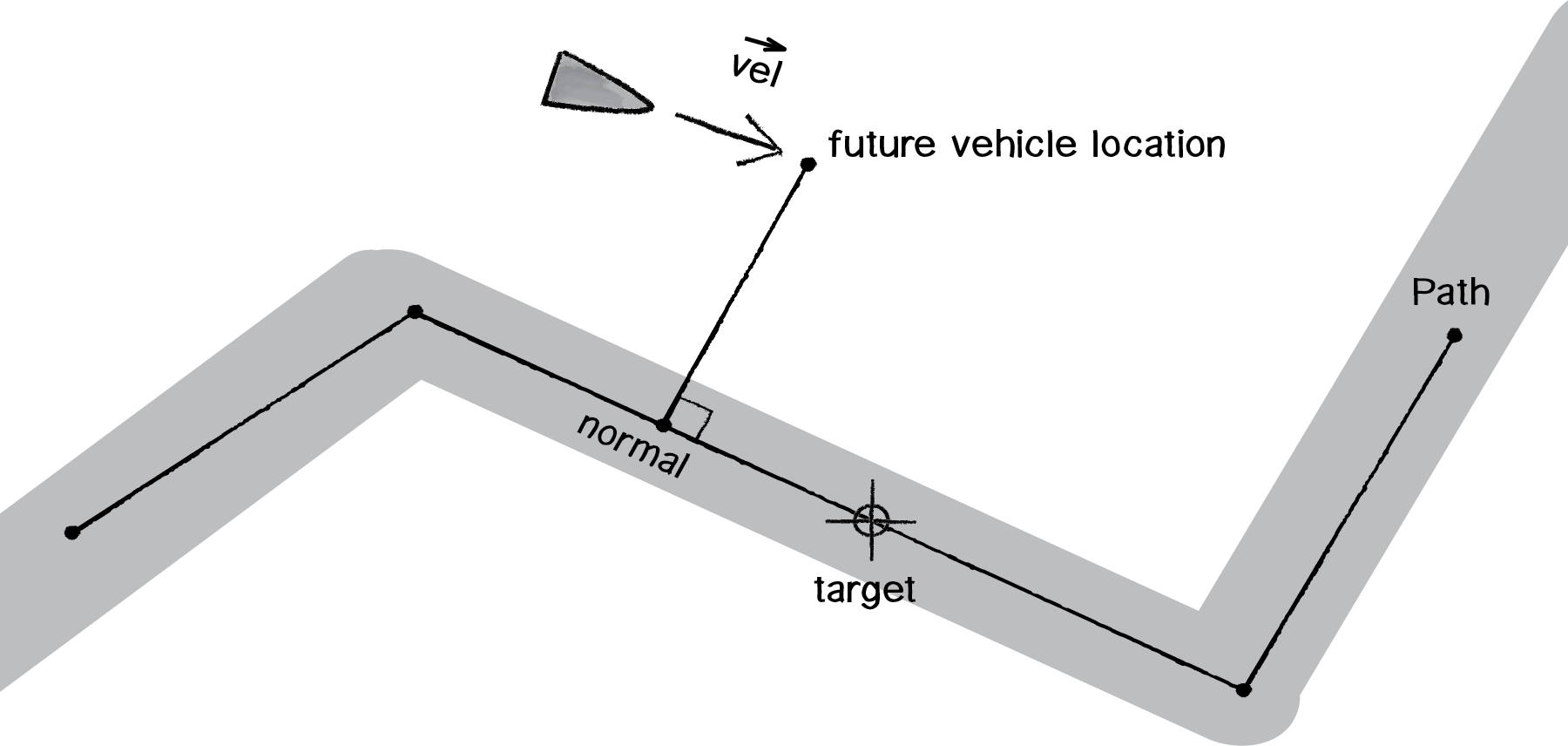
Figure 6.20
We’ll first define what we mean by a path. There are many ways we could implement a path, but for us, a simple way will be to define a path as a series of connected points:

Figure 6.21
An even simpler path would be a line between two points.
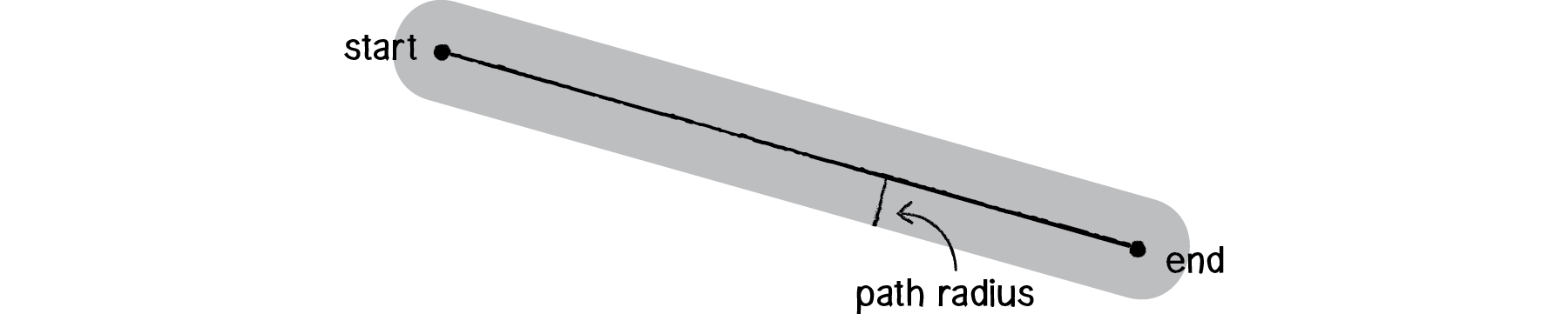
Figure 6.22
We’re also going to consider a path to have a radius. If we think of the path as a road, the radius determines the road’s width. With a smaller radius, our vehicles will have to follow the path more closely; a wider radius will allow them to stray a bit more.
Putting this into a class, we have:
public class Path6_5 : MonoBehaviour
{
public Transform startVector, endVector;
public float radius;
public Material pathMaterial;
void Start()
{
// Create a mesh for the path.
GameObject path = GameObject.CreatePrimitive(PrimitiveType.Quad);
Destroy(path.GetComponent<meshcollider>());
path.GetComponent<renderer>().material = pathMaterial;
// Align the mesh to the path.
// Center the path to the midpoint of the track start and end:
path.transform.position = 0.5f * (startVector.position + endVector.position);
// Scale the path to reflect the path length and radius:
path.transform.localScale = new Vector3(
radius * 2,
Vector3.Distance(startVector.position, endVector.position),
1
);
// Rotate the path to align it to the angle between the start and end:
path.transform.eulerAngles =
Vector3.forward * Vector3.Angle(Vector3.down, endVector.position - startVector.position);
}
}
Now, let’s assume we have a vehicle (as depicted below) outside of the path’s radius, moving with a velocity.
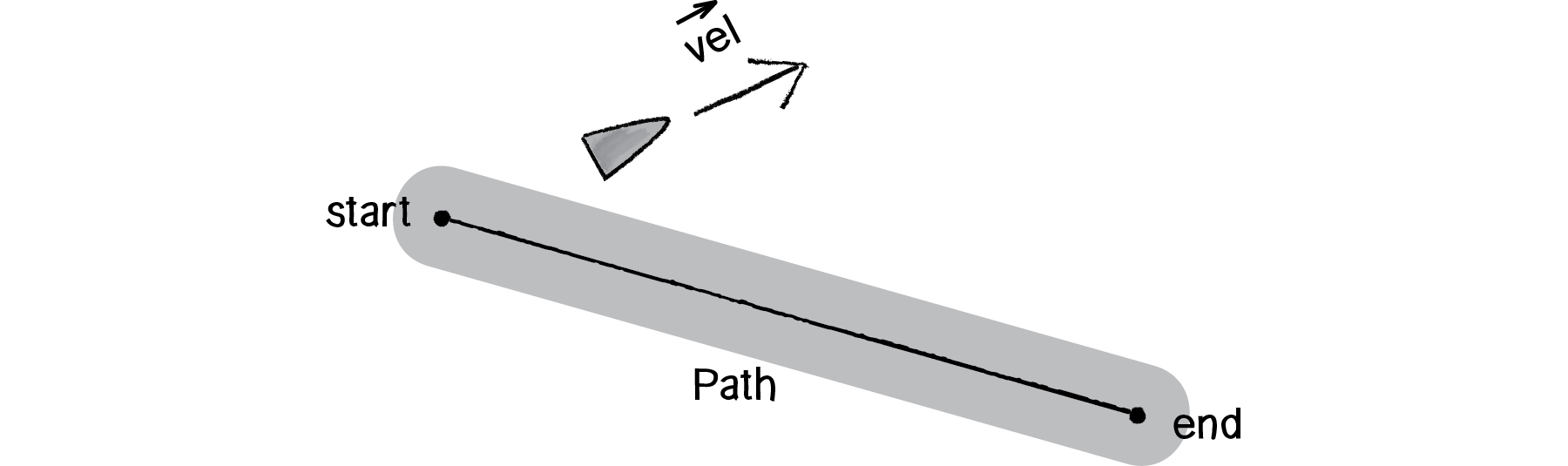
Figure 6.23
The first thing we want to do is predict, assuming a constant velocity, where that vehicle will be in the future.
// Predict the future location of the body.
Vector2 predictedLocation = body.position + body.velocity.normalized * 2.5f;
Once we have that location, it’s now our job to find out the vehicle’s current distance from the path of that predicted location. If it’s very far away, well, then, we’ve strayed from the path and need to steer back towards it. If it’s close, then we’re doing OK and are following the path nicely.
So, how do we find the distance between a point and a line? This concept is key. The distance between a point and a line is defined as the length of the normal between that point and line. The normal is a vector that extends from that point and is perpendicular to the line.
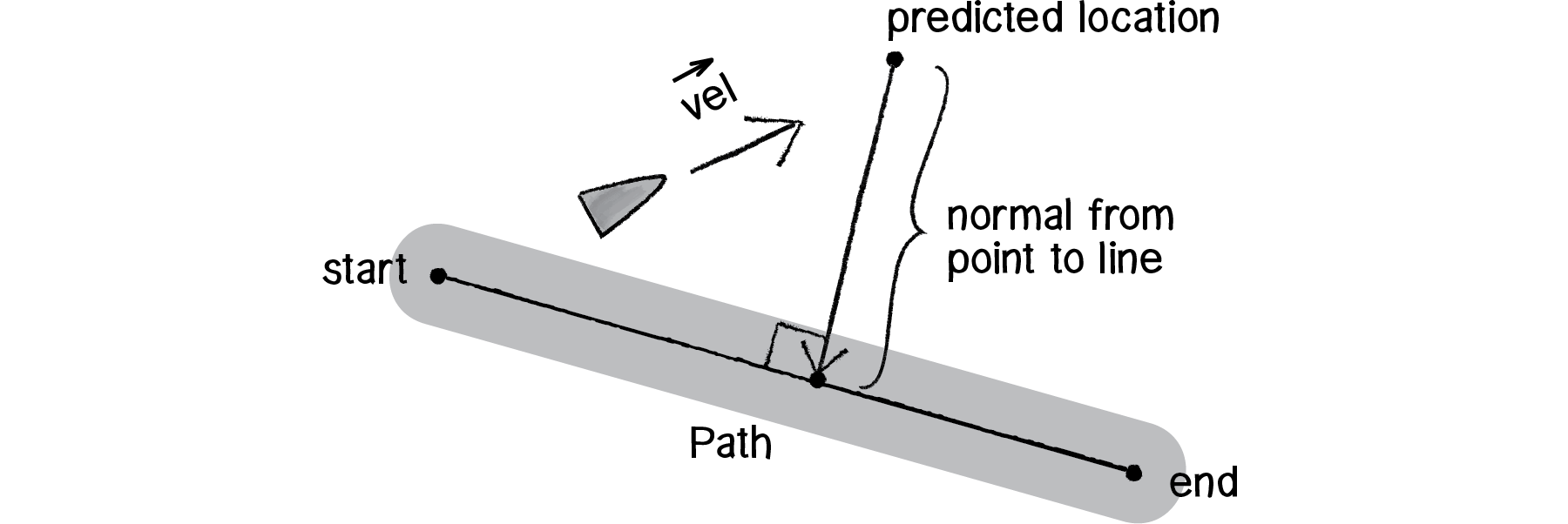
Figure 6.24
Let’s figure out what we do know. We know we have a vector (call it A→) that extends from the path’s starting point to the vehicle’s predicted location.
// Find the closest point along the path:
Vector2 a = path.startVector.position;
Vector2 b = path.endVector.position;
// Determine a follow target some distance further down the path.
Vector2 pathDirection = b - a;
We also know that we can define a vector (call it B→) that points from the start of the path to the end.
// Determine a follow target some distance further down the path.
Vector2 pathDirection = b - a;
Vector2 alongPath = pathDirection.normalized * 2.5f;
Vector2 target = normalPoint + alongPath;
Now, with basic trigonometry, we know that the distance from the path’s start to the normal point is: |A| * cos(theta).
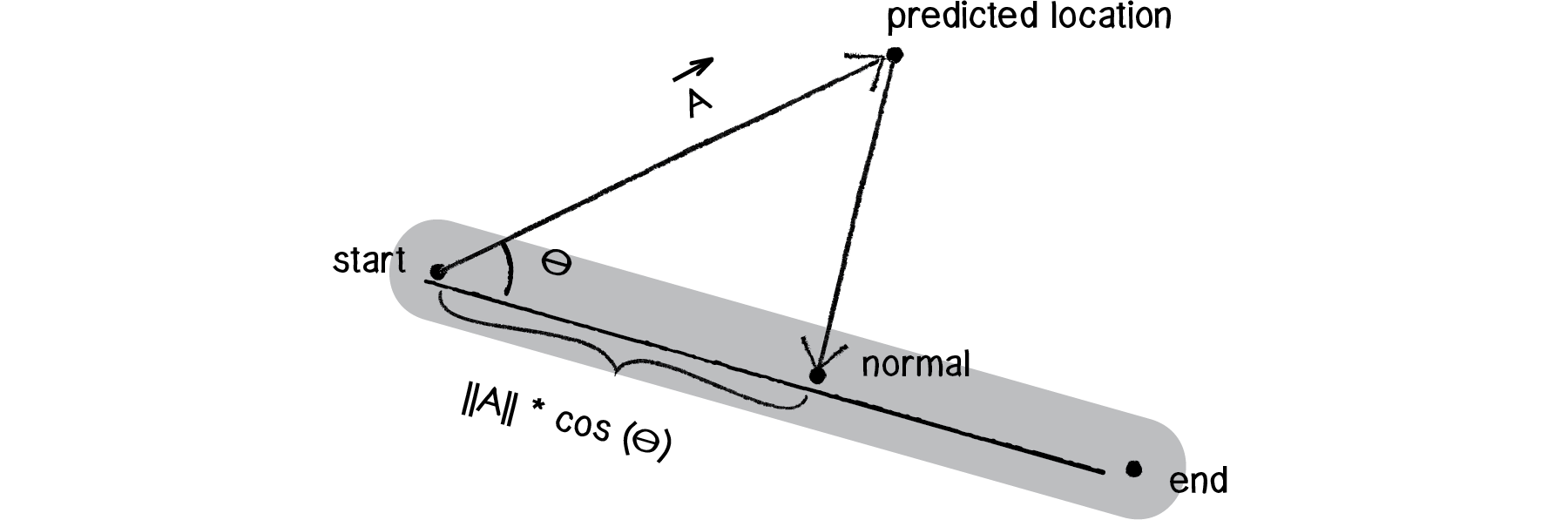
Figure 6.25
If we knew theta, we could easily define that normal point as follows:
// Predict the future location of the body.
Vector2 predictedLocation = body.position + body.velocity.normalized * 2.5f;
// Find the closest point along the path:
Vector2 a = path.startVector.position;
Vector2 b = path.endVector.position;
Vector2 normalPoint = GetNormalPoint(predictedLocation, a, b);
And if the dot product has taught us anything, it’s that given two vectors, we can get theta, the angle between.
Vector2 normalPoint = GetNormalPoint(predictedLocation, a, b);
private Vector2 GetNormalPoint(Vector2 point, Vector2 start, Vector2 end)
{
// Treat start as the origin of our problem.
Vector2 ap = point - start;
Vector2 ab = end - start;
// Scale the vector by the dot product to find the nearest point to p.
ab.Normalize();
ab *= Vector2.Dot(ap, ab);
// Re-add the relative position of our input.
Vector2 normalPoint = ab + start;
return normalPoint;
}
While the above code will work, there’s one more simplification we can make. If you’ll notice, the desired magnitude for vector B→ is:
a.mag()*cos(theta)which is the code translation of:
∥A→∥ * cos(θ)
And if you recall:
A→ · B→ = ∥A→∥ * ∥B→∥ * cos(θ)
Now, what if vector B→ is a unit vector, i.e. length 1? Then:
A→ · B→ = ∥A→∥ * 1 * cos(θ)
or
A→ · B→ = ∥A→∥ * cos(θ)
And what are we doing in our code? Normalizing ab!
ab.Normalize();
Because of this fact, we can simplify our code as:
// Scale the vector by the dot product to find the nearest point to p.
ab.Normalize();
ab *= Vector2.Dot(ap, ab);
// Re-add the relative position of our input.
Vector2 normalPoint = ab + start;
This process is commonly known as “scalar projection.” |A| cos(θ) is the scalar projection of A onto B.
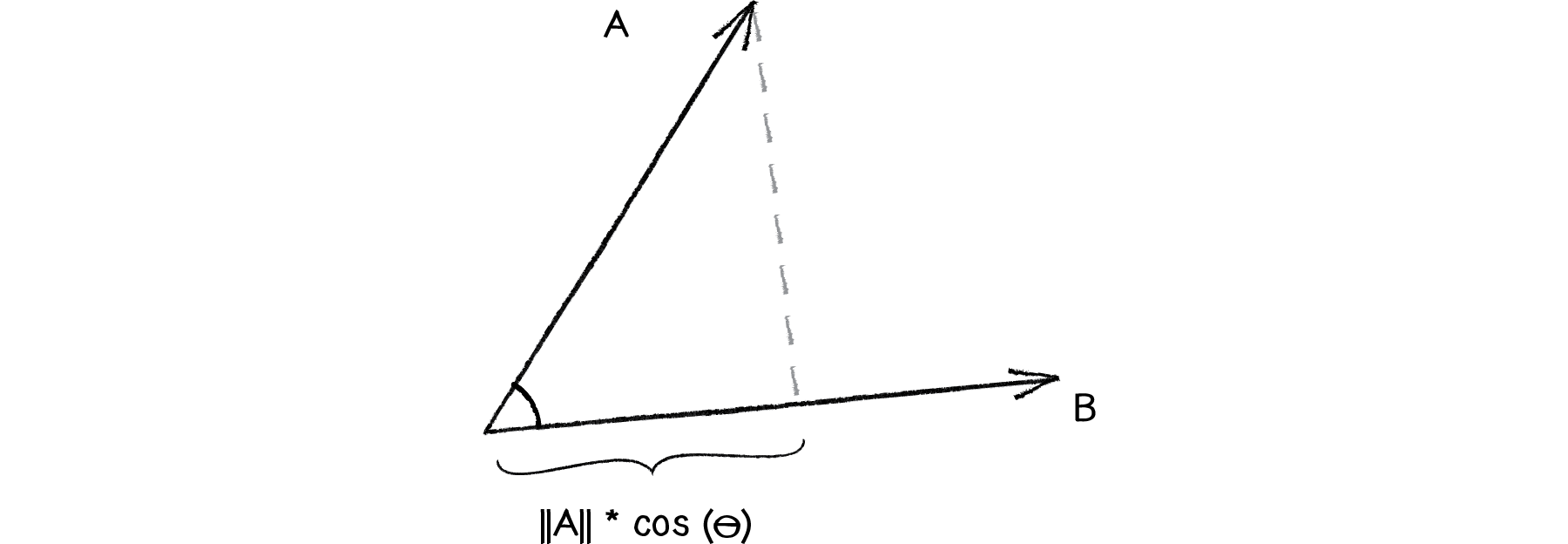
Figure 6.26
Once we have the normal point along the path, we have to decide whether the vehicle should steer towards the path and how. Reynolds’s algorithm states that the vehicle should only steer towards the path if it strays beyond the path (i.e., if the distance between the normal point and the predicted future location is greater than the path radius).
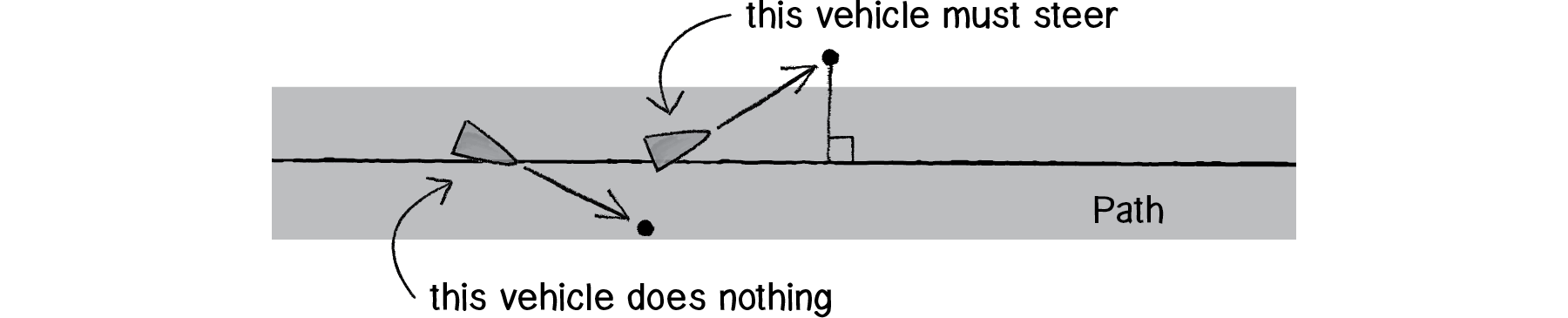
Figure 6.27
// Is the vehicle predicted to leave the path?
float distance = Vector2.Distance(normalPoint, predictedLocation);
if(distance > path.radius)
{
// If so, steer the vehicle towards the path.
Seek(target);
}
But what is the target?
Reynolds’s algorithm involves picking a point ahead of the normal on the path (see step #3 above). But for simplicity, we could just say that the target is the normal itself. This will work fairly well:
// Is the vehicle predicted to leave the path?
float distance = Vector2.Distance(normalPoint, predictedLocation);
if(distance > path.radius)
{
// If so, steer the vehicle towards the path.
Seek(normalPoint);
}
Since we know the vector that defines the path (we’re calling it “B”), we can implement Reynolds’s “point ahead on the path” without too much trouble.
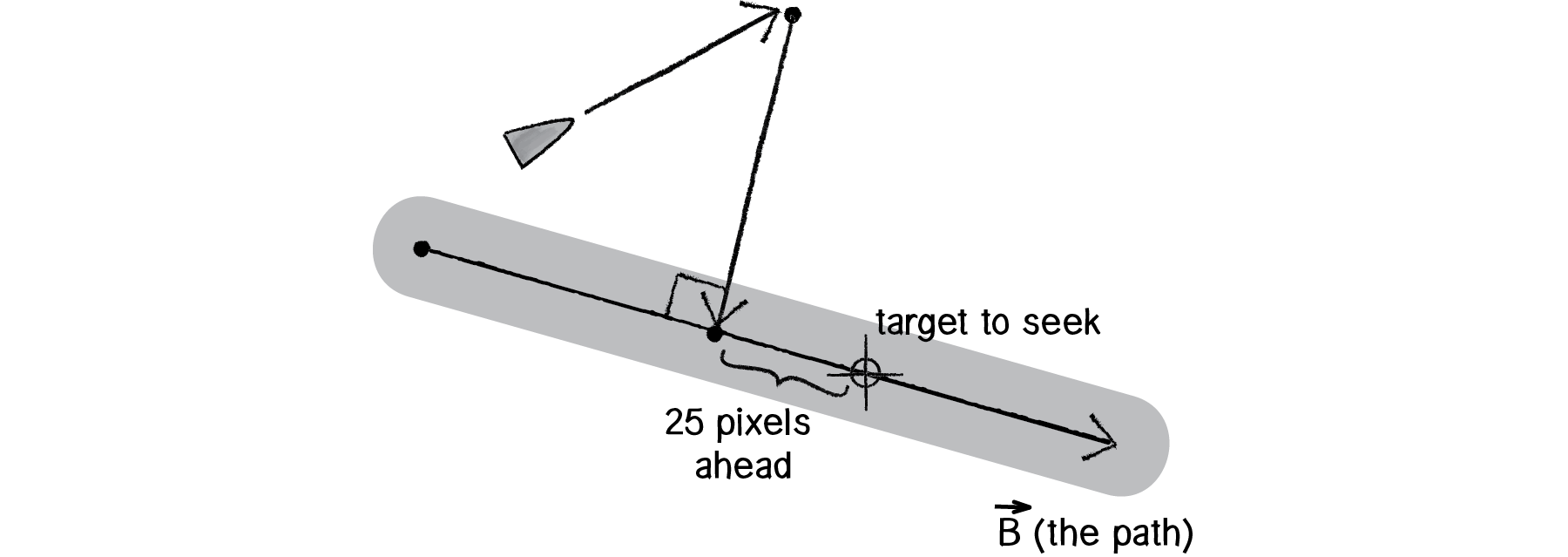
Figure 6.28
Vector2 target = normalPoint + alongPath;
// Is the vehicle predicted to leave the path?
float distance = Vector2.Distance(normalPoint, predictedLocation);
if(distance > path.radius)
{
// If so, steer the vehicle towards the path.
Seek(target);
}
Putting it all together, we have the following steering function in our Vehicle class.
Example 6.5: Simple path following
Now, you may notice above that instead of using all that dot product/scalar projection code to find the normal point, we instead call a function: getNormalPoint(). In cases like this, it’s useful to break out the code that performs a specific task (finding a normal point) into a function that it can be used generically in any case where it is required. The function takes three Vector3s: the first defines a point in Cartesian space and the second and third arguments define a line segment.
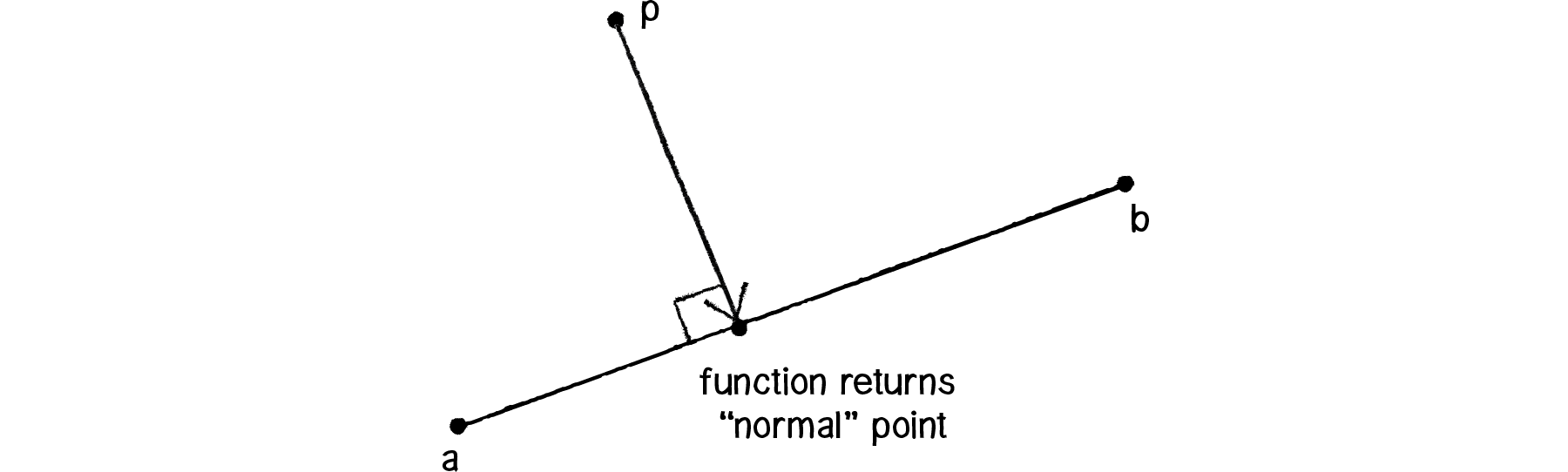
Figure 6.29
private Vector2 GetNormalPoint(Vector2 point, Vector2 start, Vector2 end)
{
// Treat start as the origin of our problem.
Vector2 ap = point - start;
Vector2 ab = end - start;
// Scale the vector by the dot product to find the nearest point to p.
ab.Normalize();
ab *= Vector2.Dot(ap, ab);
// Re-add the relative position of our input.
Vector2 normalPoint = ab + start;
return normalPoint;
}
What do we have so far? We have a Path class that defines a path as a line between two points. We have a Vehicle class that defines a vehicle that can follow the path (using a steering behavior to seek a target along the path). What is missing?
Take a deep breath. We’re almost there.
6.9 Path Following with Multiple Segments

Figure 6.30
We’ve built a great example so far, yes, but it’s pretty darn limiting. After all, what if we want our path to be something that looks more like:

Figure 6.31
While it’s true that we could make this example work for a curved path, we’re much less likely to end up needing a cool compress on our forehead if we stick with line segments. In the end, we can always employ the same technique we discovered with Box2D—we can draw whatever fancy curved path we want and approximate it behind the scenes with simple geometric forms.
So, what’s the problem? If we made path following work with one line segment, how do we make it work with a series of connected line segments? Let’s take a look again at our vehicle driving along the screen. Say we arrive at Step 3.
Step 3: Find a target point on the path.
To find the target, we need to find the normal to the line segment. But now that we have a series of line segments, we have a series of normal points (see above)! Which one do we choose? The solution we’ll employ is to pick the normal point that is (a) closest and (b) on the path itself.
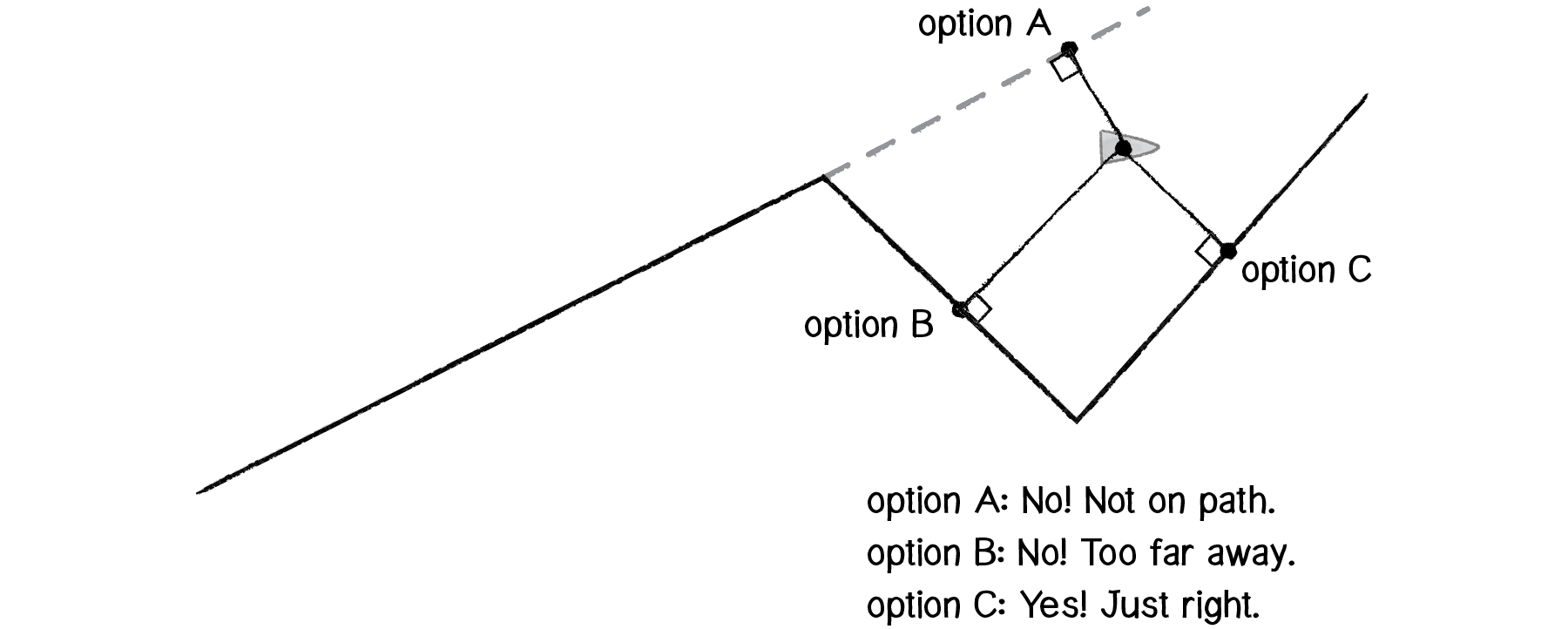
Figure 6.32
If we have a point and an infinitely long line, we’ll always have a normal. But, as in the path-following example, if we have a point and a line segment, we won’t necessarily find a normal that is on the line segment itself. So if this happens for any of the segments, we can disqualify those normals. Once we are left with normals that are on the path itself (only two in the above diagram), we simply pick the one that is closest to our vehicle’s location.
In order to write the code for this, we’ll have to expand our Path class to have a List of points (rather than just two, a start and an end).
public class Path6_6 : MonoBehaviour
{
public Transform[] points;
public float radius;
public Material pathMaterial;
private LineRenderer pathRenderer;
// Start is called before the first frame update
void Start()
{
// Create a line renderer to draw the path.
pathRenderer = new GameObject().AddComponent>linerenderer<();
pathRenderer.generateLightingData = true;
pathRenderer.material = pathMaterial;
pathRenderer.widthMultiplier = radius * 2;
// Get the path positions from the transforms.
pathRenderer.positionCount = points.Length;
for(int i = 0; i < points.Length; i++)
{
pathRenderer.SetPosition(i, points[i].position);
}
}
}
Now that we have the Path class defined, it’s the vehicle’s turn to deal with multiple line segments. All we did before was find the normal for one line segment. We can now find the normals for all the line segments in a loop.
for(int i = 0; i < path.points.Length - 1; i++)
{
Vector2 a = path.points[i].position;
Vector2 b = path.points[i + 1].position;
Vector2 normalPoint = GetNormalPoint(predictedLocation, a, b);
}
Then we should make sure the normal point is actually between points a and b. Since we know our path goes from left to right in this example, we can test if the x component of normalPoint is outside the x components of a and b.
// If the normal point is beyond the line segment, clamp it to the endpoint.
if(normalPoint.x > b.x || normalPoint.x < a.x)
{
normalPoint = b;
}
As a little trick, we’ll say that if it’s not within the line segment, let’s just pretend the end point of that line segment is the normal. This will ensure that our vehicle always stays on the path, even if it strays out of the bounds of our line segments.
Finally, we’ll need to make sure we find the normal point that is closest to our vehicle. To accomplish this, we start with a very high “world record” distance and iterate through each normal point to see if it beats the record (i.e. is less than). Each time a normal point beats the record, the world record is updated and the winning point is stored in a variable named target. At the end of the loop, we’ll have the closest normal point in that variable.
Example 6.6: Path following
Exercise 6.10
Update the path-following example so that the path can go in any direction. (Hint: you’ll need to change the points array of Transforms into a List a and create a method to determine if the normal point is inside the line segment.)
Exercise 6.11
Create a path that changes over time. Can the points that define the path itself have their own steering behaviors?
6.10 Complex Systems
Remember our purpose? To breathe life into the things that move around our Unity windows? By learning to write the code for an autonomous agent and building a series of examples of individual behaviors, hopefully our souls feel a little more full. But this is no place to stop and rest on our laurels. We’re just getting started. After all, there is a deeper purpose at work here. Yes, a vehicle is a simulated being that makes decisions about how to seek and flow and follow. But what is a life led alone, without the love and support of others? Our purpose here is not only to build individual behaviors for our vehicles, but to put our vehicles into systems of many vehicles and allow those vehicles to interact with each other.
Let’s think about a tiny, crawling ant—one single ant. An ant is an autonomous agent; it can perceive its environment (using antennae to gather information about the direction and strength of chemical signals) and make decisions about how to move based on those signals. But can a single ant acting alone build a nest, gather food, defend its queen? An ant is a simple unit and can only perceive its immediate environment. A colony of ants, however, is a sophisticated complex system, a “superorganism” in which the components work together to accomplish difficult and complicated goals.
We want to take what we’ve learned during the process of building autonomous agents in Unity into simulations that involve many agents operating in parallel—agents that have an ability to perceive not only their physical environment but also the actions of their fellow agents, and then act accordingly. We want to create complex systems in Unity.
What is a complex system? A complex system is typically defined as a system that is “more than the sum of its parts.” While the individual elements of the system may be incredibly simple and easily understood, the behavior of the system as a whole can be highly complex, intelligent, and difficult to predict. Here are three key principles of complex systems.
Simple units with short-range relationships. This is what we’ve been building all along: vehicles that have a limited perception of their environment.
Simple units operate in parallel. This is what we need to simulate in code. For every cycle through Unity’s Update() loop, each unit will decide how to move (to create the appearance of them all working in parallel).
System as a whole exhibits emergent phenomena. Out of the interactions between these simple units emerges complex behavior, patterns, and intelligence. Here we’re talking about the result we are hoping for in our scenees. Yes, we know this happens in nature (ant colonies, termites, migration patterns, earthquakes, snowflakes, etc.), but can we achieve the same result in our Unity scenees?
Following are three additional features of complex systems that will help frame the discussion, as well as provide guidelines for features we will want to include in our software simulations. It’s important to acknowledge that this is a fuzzy set of characteristics and not all complex systems have all of them.
Non-linearity. This aspect of complex systems is often casually referred to as “the butterfly effect,” coined by mathematician and meteorologist Edward Norton Lorenz, a pioneer in the study of chaos theory. In 1961, Lorenz was running a computer weather simulation for the second time and, perhaps to save a little time, typed in a starting value of 0.506 instead of 0.506127. The end result was completely different from the first result of the simulation. In other words, the theory is that a single butterfly flapping its wings on the other side of the world could cause a massive weather shift and ruin our weekend at the beach. We call it “non-linear” because there isn’t a linear relationship between a change in initial conditions and a change in outcome. A small change in initial conditions can have a massive effect on the outcome. Non-linear systems are a superset of chaotic systems. In the next chapter, we’ll see how even in a system of many zeros and ones, if we change just one bit, the result will be completely different.
Competition and cooperation. One of the things that often makes a complex system tick is the presence of both competition and cooperation between the elements. In our upcoming flocking system, we will have three rules—alignment, cohesion, and separation. Alignment and cohesion will ask the elements to “cooperate”—i.e. work together to stay together and move together. Separation, however, will ask the elements to “compete” for space. As we get to the flocking system, try taking out the cooperation or the competition and you’ll see how you are left without complexity. Competition and cooperation are found in living complex systems, but not in non-living complex systems like the weather.
Feedback. Complex systems often include a feedback loop where the the output of the system is fed back into the system to influence its behavior in a positive or negative direction. Let’s say you drive to work each day because the price of gas is low. In fact, everyone drives to work. The price of gas goes up as demand begins to exceed supply. You, and everyone else, decide to take the train to work because driving is too expensive. And the price of gas declines as the demand declines. The price of gas is both the input of the system (determining whether you choose to drive or ride the train) and the output (the demand that results from your choice). I should note that economic models (like supply/demand, the stock market) are one example of a human complex system. Others include fads and trends, elections, crowds, and traffic flow.
Complexity will serve as a theme for the remaining content in this book. In this chapter, we’ll begin by adding one more feature to our Vehicle class: an ability to look at neighboring vehicles.
6.11 Group Behaviors (or: Let’s not run into each other)
A group is certainly not a new concept. We’ve done this before—in Chapter 4, where we developed a framework for managing collections of particles in a ParticleSystem class. There, we stored a list of particles in a List. We’ll do the same thing here: store a bunch of Vehicle objects in a List.
public class Chapter6Fig7 : MonoBehaviour
{
public float maxSpeed = 2, maxForce = 2;
private List<vehicle> vehicles; // Declare a List of Vehicle objects.
private Vector2 minimumPos, maximumPos;
void Start()
{
findWindowLimits();
vehicles = new List<vehicle>(); // Initilize and fill the List with a bunch of Vehicles
for (int i = 0; i < 100; i++) {
float ranX = Random.Range(minimumPos.x, maximumPos.x);
float ranY = Random.Range(minimumPos.y, maximumPos.y);
vehicles.Add(new Vehicle(new Vector2(ranX, ranY), minimumPos, maximumPos, maxSpeed, maxForce));
}
}
}
Now when it comes time to deal with all the vehicles in Update(), we simply loop through all of them and call the necessary functions.
void Update()
{
foreach (Vehicle v in vehicles)
{
v.Separate(vehicles);
v.CheckEdges();
}
}
OK, so maybe we want to add a behavior, a force to be applied to all the vehicles. This could be seeking the mouse.
Vector2 mousePos = Input.mousePosition;
mousePos = Camera.main.ScreenToWorldPoint(mousePos);
v.Seek(mousePos);
But that’s an individual behavior. We’ve already spent thirty-odd pages worrying about individual behaviors. We’re here because we want to apply a group behavior. Let’s begin with separation, a behavior that commands, “Avoid colliding with your neighbors!”
v.Separate();
Is that right? It sounds good, but it’s not. What’s missing? In the case of seek, we said, “Seek mouseX and mouseY.” In the case of separate, we’re saying “separate from everyone else.” Who is everyone else? It’s the list of all the other vehicles.
v.Separate(vehicles);
This is the big leap beyond what we did before with particle systems. Instead of having each element (particle or vehicle) operate on its own, we’re now saying, “Hey you, the vehicle! When it comes time for you to operate, you need to operate with an awareness of everyone else. So I’m going to go ahead and pass you the List of everyone else.”
This is how we’ve mapped out setup() and draw() to deal with a group behavior.
public class Chapter6Fig7 : MonoBehaviour
{
public float maxSpeed = 2, maxForce = 2;
private List<vehicle> vehicles; // Declare a List of Vehicle objects.
private Vector2 maximumPos;
void Start()
{
FindWindowLimits();
vehicles = new List<vehicle>(); // Initilize and fill the List with a bunch of Vehicles
for (int i = 0; i < 100; i++) {
float ranX = Random.Range(minimumPos.x, maximumPos.x);
float ranY = Random.Range(minimumPos.y, maximumPos.y);
vehicles.Add(new Vehicle(new Vector2(ranX, ranY), minimumPos, maximumPos, maxSpeed, maxForce));
}
}
void Update()
{
foreach (Vehicle v in vehicles)
{
v.Separate(vehicles);
v.CheckEdges();
}
if (Input.GetMouseButton(0))
{
Vector2 mousePos = Input.mousePosition;
mousePos = Camera.main.ScreenToWorldPoint(mousePos);
vehicles.Add(new Vehicle(mousePos, minimumPos, maximumPos, maxSpeed, maxForce));
}
}
private void FindWindowLimits()
{
// We want to start by setting the camera's projection to Orthographic mode
Camera.main.orthographic = true;
// For FindWindowLimits() to function correctly, the camera must be set to coordinates 0, 0, -10
Camera.main.transform.position = new Vector3(0, 0, -5);
// Next we grab the maximum position for the screen
maximumPos = Camera.main.ScreenToWorldPoint(new Vector2(Screen.width, Screen.height));
}
}

Figure 6.33
Of course, this is just the beginning. The real work happens inside the separate() function itself. Let’s figure out how we want to define separation. Reynolds states: “Steer to avoid crowding.” In other words, if a given vehicle is too close to you, steer away from that vehicle. Sound familiar? Remember the seek behavior where a vehicle steers towards a target? Reverse that force and we have the flee behavior.
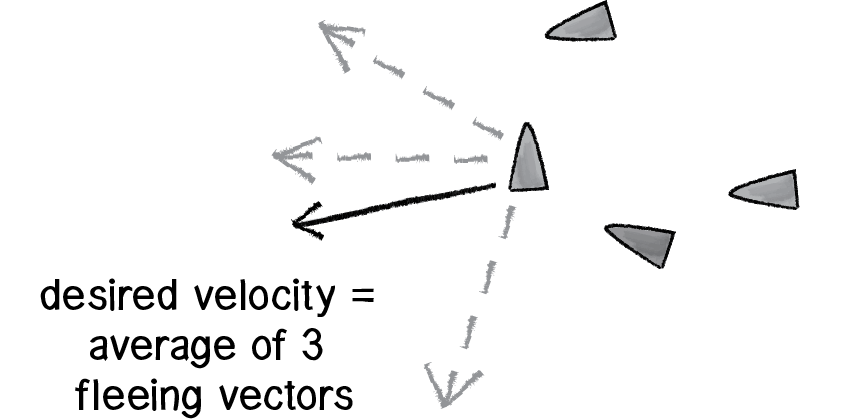
Figure 6.34
But what if more than one vehicle is too close? In this case, we’ll define separation as the average of all the vectors pointing away from any close vehicles.
Let’s begin to write the code. As we just worked out, we’re writing a function called separate() that receives a List of Vehicle objects as an argument.
public void Separate(List<vehicle> vehicles)
{
}
Inside this function, we’re going to loop through all of the vehicles and see if any are too close.
public void Separate(List<vehicle> vehicles)
{
// Note how the desired separation is based on the Vehicle's size.
float desiredSeparation = myVehicle.transform.localScale.x * 2;
foreach (Vehicle other in vehicles)
{
// What is the distance between me and another Vehicle?
float d = Vector2.Distance(other.location, location);
if ((d > 0) && (d < desiredSeparation))
{
}
}
}
Notice how in the above code, we are not only checking if the distance is less than a desired separation (i.e. too close!), but also if the distance is greater than zero. This is a little trick that makes sure we don’t ask a vehicle to separate from itself. Remember, all the vehicles are in the List, so if you aren’t careful you’ll be comparing each vehicle to itself!
Once we know that two vehicles are too close, we need to make a vector that points away from the offending vehicle.
if ((d > 0) && (d < desiredSeperation))
{
// Any code here will be executed if the Vehicle is within 0.5 Meters.
Vector2 diff = location - other.location; // A Vector2 pointing away from the other’s location.
diff.Normalize();
}
This is not enough. We have that vector now, but we need to make sure we calculate the average of all vectors pointing away from close vehicles. How do we compute average? We add up all the vectors and divide by the total.
public void Separate(List<vehicle> vehicles)
{
Vector2 sum = Vector2.zero; // Start with a blank Vector2.
int count = 0; // We have to keep track of how many Vehicles are too close.
// Note how the desired separation is based on the Vehicle's size.
float desiredSeparation = myVehicle.transform.localScale.x * 2;
foreach (Vehicle other in vehicles)
{
// What is the distance between me and another Vehicle?
float d = Vector2.Distance(other.location, location);
if ((d > 0) && (d < desiredSeparation))
{
// Any code here will be executed if the Vehicle is within 0.5 Meters.
Vector2 diff = location - other.location; // A Vector2 pointing away from the other’s location.
diff.Normalize();
/* What is the magnitude of the PVector pointing away
* from the other vehicle? The closer it is, the more we
* should flee. The farther, the less. So we divide by the
* distance to weight it appropriately. */
diff /= d;
sum += diff; // Add all the vectors together and increment the count
count++;
}
}
/* We have to make sure we found at least one close vehicle.
* We don't want to bother doing anything if nothing is
* too close (not to mention we can't divide by zero!) */
if (count > 0)
{
sum /= count;
}
}
We have to make sure we found at least one close vehicle. We don’t want to bother doing anything if nothing is too close (not to mention we can’t divide by zero!)
if (count > 0) { sum.div(count); }Once we have the average vector (stored in the Vector3 object “sum”), that Vector3 can be scaled to maximum speed and become our desired velocity—we desire to move in that direction at maximum speed! And once we have the desired velocity, it’s the same old Reynolds story: steering equals desired minus velocity.
/* We have to make sure we found at least one close vehicle.
* We don't want to bother doing anything if nothing is
* too close (not to mention we can't divide by zero!) */
if (count > 0)
{
sum /= count;
sum *= maxSpeed; // Scale averate to maxSpeed (this becomes desired).
Vector2 steer = sum - velocity; // Reynold's steering formula
steer = Vector2.ClampMagnitude(steer, maxForce); // Clamp to the maximum force.
rb.AddForce(steer); // Apply the force to the Vehicle's acceleration.
}
Let’s see the function in its entirety. There are two additional improvements, noted in the code comments.
Example 6.7: Group behavior: Separation
Exercise 6.12
Rewrite Separate() to work in the opposite fashion (“cohesion”). If a vehicle is beyond a certain distance, steer towards that vehicle. This will keep the group together. (Note that in a moment, we’re going to look at what happens when we have both cohesion and separation in the same simulation.)
Exercise 6.13
Add the separation force to path following to create a simulation of Reynolds’s “Crowd Path Following.”
6.12 Combinations
The previous two exercises hint at what is perhaps the most important aspect of this chapter. After all, what is a Unity scene with one steering force compared to one with many? How could we even begin to simulate emergence in our scenees with only one rule? The most exciting and intriguing behaviors will come from mixing and matching multiple steering forces, and we’ll need a mechanism for doing so.
You may be thinking, “Duh, this is nothing new. We do this all the time.” You would be right. In fact, we did this as early as Chapter 2.
void FixedUpdate()
{
// Apply the forces to each of the Movers
foreach (Mover2_2 mover in Movers)
{
// ForceMode.Impulse takes mass into account
mover.body.AddForce(wind, ForceMode.Impulse);
mover.body.AddForce(gravity, ForceMode.Force);
mover.CheckBoundaries();
}
}
Here we have a mover that responds to two forces. This all works nicely because of the way we designed the Mover class to accumulate the force vectors into its acceleration vector. In this chapter, however, our forces stem from internal desires of the movers (now called vehicles). And those desires can be weighted. Let’s consider a scene where all vehicles have two desires:
Seek the mouse location.
Separate from any vehicles that are too close.
Here we see how a single loop takes care of calling the other functions that apply the forces—separate() and seek(). We could start mucking around with those functions and see if we can adjust the strength of the forces they are calculating. But it would be easier for us to ask those functions to return the forces so that we can adjust their strength before applying them to the vehicle’s acceleration.
void Update()
{
Vector2 mousePos = Input.mousePosition;
mousePos = Camera.main.ScreenToWorldPoint(mousePos);
foreach (Vehicle v in vehicles)
{
Vector2 separate = v.Separate(vehicles);
Vector2 seek = v.Seek(mousePos);
}
}
Let’s look at how the seek function changed.
public Vector2 Seek(Vector2 target)
{
Vector2 desired = target - location;
desired.Normalize();
desired *= maxSpeed;
Vector2 steer = desired - velocity;
steer = Vector2.ClampMagnitude(steer, maxForce);
return steer;
}
This is a subtle change, but incredibly important for us: it allows us to alter the strength of these forces in one place.
Example 6.8: Combining steering behaviors: Seek and separate
Exercise 6.14
Redo Example 6.8 so that the behavior weights are not constants. What happens if they change over time (according to a sine wave or Perlin noise)? Or if some vehicles are more concerned with seeking and others more concerned with separating? Can you introduce other steering behaviors as well?
6.13 Flocking
Flocking is an group animal behavior that is characteristic of many living creatures, such as birds, fish, and insects. In 1986, Craig Reynolds created a computer simulation of flocking behavior and documented the algorithm in his paper, “Flocks, Herds, and Schools: A Distributed Behavioral Model.” Recreating this simulation in Unity will bring together all the concepts in this chapter.
We will use the steering force formula (steer = desired - velocity) to implement the rules of flocking.
These steering forces will be group behaviors and require each vehicle to look at all the other vehicles.
We will combine and weight multiple forces.
The result will be a complex system—intelligent group behavior will emerge from the simple rules of flocking without the presence of a centralized system or leader.
The good news is, we’ve already done items 1 through 3 in this chapter, so this section will be about just putting it all together and seeing the result.
Before we begin, I should mention that we’re going to change the name of our Vehicle class (yet again). Reynolds uses the term “boid” (a made-up word that refers to a bird-like object) to describe the elements of a flocking system and we will do the same.
Let’s take an overview of the three rules of flocking.
Separation (also known as “avoidance”): Steer to avoid colliding with your neighbors.
Alignment (also known as “copy”): Steer in the same direction as your neighbors.
Cohesion (also known as “center”): Steer towards the center of your neighbors (stay with the group).
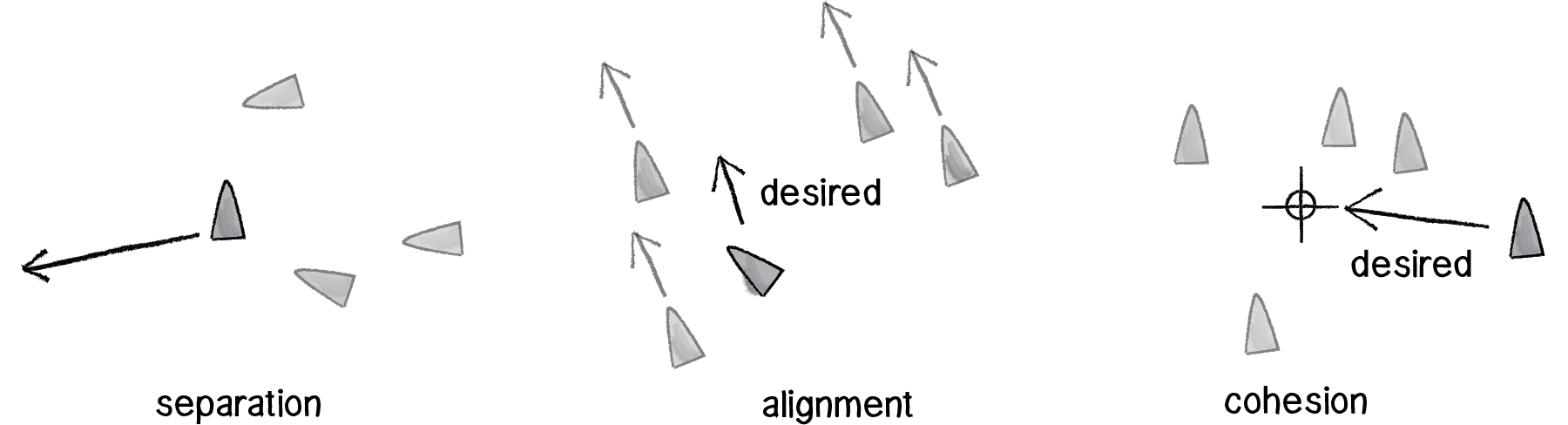
Figure 6.35
Just as we did with our separate and seek example, we’ll want our Boid objects to have a single function that manages all the above behaviors. We’ll call this function flock().
public void Flock(List<boid> boids)
{
Vector2 sep = Separate(boids); // The three flocking rules
Vector2 ali = Align(boids);
Vector2 coh = Cohesion(boids);
sep *= 5.0f; // Arbitrary weights for these forces (Try different ones!)
ali *= 1.5f;
coh *= 0.5f;
ApplyForce(sep); // Applying all the forces
ApplyForce(ali);
ApplyForce(coh);
checkBounds(); // To loop the world to the other side of the screen.
lookForward(); // Make the boids face forward.
}
Now, it’s just a matter of implementing the three rules. We did separation before; it’s identical to our previous example. Let’s take a look at alignment, or steering in the same direction as your neighbors. As with all of our steering behaviors, we’ve got to boil down this concept into a desire: the boid’s desired velocity is the average velocity of its neighbors.
So our algorithm is to calculate the average velocity of all the other boids and set that to desired.
public Vector2 Align(List<boid> boids)
{
/* Add up all the velocities and divide by the total to
* calculate the average velocity. */
Vector2 sum = Vector2.zero;
int count = 0;
foreach (Boid other in boids)
{
float d = Vector2.Distance(location, other.location);
if((d > 0) && (d < neighborDist))
{
sum += other.velocity;
}
}
if (count > 0)
{
sum /= count;
sum = sum.normalized * maxSpeed; // We desite to go in that direction at maximum speed.
Vector2 steer = sum - velocity; // Reynolds's steering force formula.
steer = Vector2.ClampMagnitude(steer, maxForce);
return steer;
}
}
The above is pretty good, but it’s missing one rather crucial detail. One of the key principles behind complex systems like flocking is that the elements (in this case, boids) have short-range relationships. Thinking about ants again, it’s pretty easy to imagine an ant being able to sense its immediate environment, but less so an ant having an awareness of what another ant is doing hundreds of feet away. The fact that the ants can perform such complex collective behavior from only these neighboring relationships is what makes them so exciting in the first place.
In our alignment function, we’re taking the average velocity of all the boids, whereas we should really only be looking at the boids within a certain distance. That distance threshold is up to you, of course. You could design boids that can see only twenty pixels away or boids that can see a hundred pixels away.
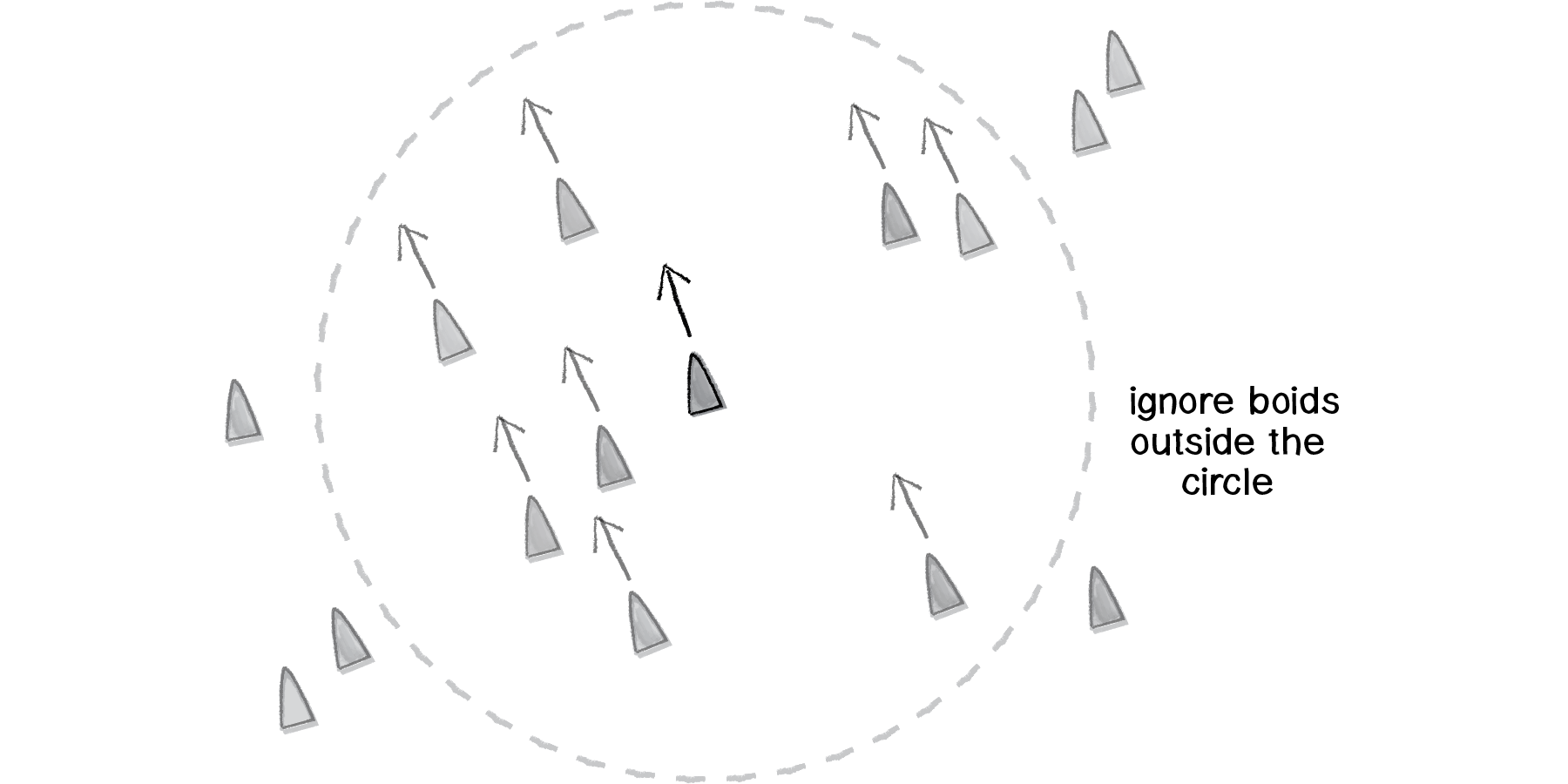
Figure 6.36
Much like we did with separation (only calculating a force for others within a certain distance), we’ll want to do the same with alignment (and cohesion).
public Vector2 Align(List<boid> boids)
{
float neighborDist = 6f; // This is an arbitrary value and could vary from boid to boid.
/* Add up all the velocities and divide by the total to
* calculate the average velocity. */
Vector2 sum = Vector2.zero;
int count = 0;
foreach (Boid other in boids)
{
float d = Vector2.Distance(location, other.location);
if((d > 0) && (d < neighborDist))
{
sum += other.velocity;
count++; // For an average, we need to keep track of how many boids are within the distance.
}
}
if (count > 0)
{
sum /= count;
sum = sum.normalized * maxSpeed; // We desite to go in that direction at maximum speed.
Vector2 steer = sum - velocity; // Reynolds's steering force formula.
steer = Vector2.ClampMagnitude(steer, maxForce);
return steer;
}
else
{
return Vector2.zero; // If we don't find any close boids, the steering force is Zero.
}
}
Exercise 6.15
Can you write the above code so that boids can only see other boids that are actually within their “peripheral” vision (as if they had eyes)?
Finally, we are ready for cohesion. Here our code is virtually identical to that for alignment—only instead of calculating the average velocity of the boid’s neighbors, we want to calculate the average location of the boid’s neighbors (and use that as a target to seek).
public Vector2 Cohesion(List<boid> boids)
{
float neighborDist = 6f;
Vector2 sum = Vector2.zero;
int count = 0;
foreach (Boid other in boids)
{
float d = Vector2.Distance(location, other.location);
if ((d > 0) && (d < neighborDist))
{
sum += other.location; // Adding up all the other's locations
count++;
}
}
if (count > 0)
{
sum /= count;
/* Here we make use of the Seek() function we wrote in
* Example 6.8. The target we seek is thr average
* location of our neighbors. */
return Seek(sum);
}
else
{
return Vector2.zero;
}
}
It’s also worth taking the time to write a class called Flock, which will be virtually identical to the ParticleSystem class we wrote in Chapter 4 with only one tiny change: When we call run() on each Boid object (as we did to each Particle object), we’ll pass in a reference to the entire List of boids.
class Boid
{
// To make it easier on ourselves, we use Get and Set as quick ways to get the location of the vehicle
public Vector2 location
{
get { return myVehicle.transform.position; }
set { myVehicle.transform.position = value; }
}
public Vector2 velocity
{
get { return rb.velocity; }
set { rb.velocity = value; }
}
private float maxSpeed, maxForce;
private Vector2 minPos, maxPos;
private GameObject myVehicle;
private Rigidbody rb;
public Boid(Vector2 initPos, Vector2 _minPos, Vector2 _maxPos, float _maxSpeed, float _maxForce, Mesh coneMesh)
{
minPos = _minPos - Vector2.one;
maxPos = _maxPos + Vector2.one;
maxSpeed = _maxSpeed;
maxForce = _maxForce;
myVehicle = GameObject.CreatePrimitive(PrimitiveType.Cube);
GameObject.Destroy(myVehicle.GetComponent<boxcollider>());
myVehicle.transform.position = new Vector2(initPos.x, initPos.y);
myVehicle.AddComponent<rigidbody>();
rb = myVehicle.GetComponent<rigidbody>();
rb.constraints = RigidbodyConstraints.FreezeRotation;
rb.useGravity = false; // Remember to ignore gravity!
/* We want to double check if a custom mesh is
* being used. If not, we will scale a cube up
* instead ans use that for our boids. */
if (coneMesh != null)
{
MeshFilter filter = myVehicle.GetComponent<meshfilter>();
filter.mesh = coneMesh;
}
else
{
myVehicle.transform.localScale = new Vector3(1f, 2f, 1f);
}
}
}
Example 6.9: Flocking
Exercise 6.16
Combine flocking with some other steering behaviors.
Exercise 6.17
In his book The Computational Beauty of Nature (MIT Press, 2000), Gary Flake describes a fourth rule for flocking: “View: move laterally away from any boid that blocks the view.” Have your boids follow this rule.
Exercise 6.18
Create a flocking simulation where all of the parameters (separation weight, cohesion weight, alignment weight, maximum force, maximum speed) change over time. They could be controlled by Perlin noise or by user interaction. (For example, you could use a library such as controlp5 to tie the values to slider positions.)
Exercise 6.19
Visualize the flock in an entirely different way.
The Ecosystem Project
Step 6 Exercise:
Use the concept of steering forces to drive the behavior of the creatures in your ecosystem. Some possibilities:
Create “schools” or “flocks” of creatures.
Use a seeking behavior for creatures to search for food (for chasing moving prey, consider “pursuit”).
Use a flow field for the ecosystem environment. For example, how does your system behave if the creatures live in a flowing river?
Build a creature with countless steering behaviors (as many as you can reasonably add). Think about ways to vary the weights of these behaviors so that you can dial those behaviors up and down, mixing and matching on the fly. How are creatures’ initial weights set? What rules drive how the weights change over time?
Complex systems can be nested. Can you design a single creature out of a flock of boids? And can you then make a flock of those creatures?
Complex systems can have memory (and be adaptive). Can the history of your ecosystem affect the behavior in its current state? (This could be the driving force behind how the creatures adjust their steering force weights.)

